 |
ATMOSPHERIC MODELS |
 |
ATMOSPHERIC MODELS |
For flight within an atmosphere it is necessary to know the atmospheric temperature, pressure and density at the wide range of altitudes that a vehicle might operate. This is done by developing a model of the atmosphere that represents either mean conditions or conditions specific to a particular time and place.
Considering that this web site is titled "Rocket & Space Technology", it is assumed that our interest in atmospheric modeling is to analyze or predict the flight of a rocket or missile, capsule, or spacecraft through the atmosphere of Earth or another planet. For launch and reentry, the lower and middle atmosphere is of paramount importance, as nearly all drag occurs at these altitudes (for Earth, below about 90 km). And for satellites and spacecraft in low orbit, we must have a model of the atmosphere hundreds of kilometers above the surface to predict the long-term effects that will result in eventual orbit decay. For altitudes between the middle atmosphere and low orbit, atmospheric effects are minor for the case of launch and/or controlled reentry, because the air is thin and the exposure is brief. However, in the case of a decaying orbit or an aerobraking maneuver, a good model of this layer may be necessary.
The atmosphere of Earth is a layer of gases surrounding the planet and retained by Earth's gravity. In general, air pressure and density decrease with altitude. However, temperature has a more complicated profile with altitude and may remain relatively constant or even increase with altitude in some regions. Because the general pattern of the temperature-altitude profile is constant and recognizable, the temperature behavior provides a useful metric to distinguish between atmospheric layers. In this way, Earth's atmosphere can be divided into five main layers. From lowest to highest, these layers are: troposphere, stratosphere, mesosphere, thermosphere and exosphere.
Troposphere: The troposphere begins at Earth's surface and extends to the tropopause at an average height of about 12 km, although this altitude varies from about 9 km at the poles and 17 km at the equator, with some variation due to weather. The tropopause is mostly heated by transfer of energy from the surface, so on average the lowest part is warmest and temperature decreases with altitude. The troposphere contains roughly 80% of the mass of the atmosphere and basically all weather-associated cloud types. The tropopause is the boundary between the troposphere and stratosphere.
Stratosphere: The stratosphere extends from the tropopause at an altitude of about 12 km above sea level to the stratopause at an altitude of 50 to 55 km. The atmospheric pressure at the top of the stratosphere is roughly 1/1000 the pressure at sea level. Temperature increases with height due to increased absorption of ultraviolet radiation by the ozone layer, which restricts turbulence and mixing. Although the temperature may be -60 oC at the tropopause, the top of the stratosphere is much warmer and may be near freezing.
Mesosphere: The mesosphere extends from the stratopause at an altitude of about 50 km to the mesopause at 80-85 km above sea level. It is the layer where most meteors burn up entering the atmosphere. Temperature decreases with height in the mesosphere. The mesopause, the temperature minimum that marks the top of the mesosphere, is the coldest place on Earth with an average temperature of about -85 oC, and may drop to -100 oC.
Thermosphere: Temperature increases with height in the thermosphere from the mesopause at an altitude of about 80 km up to the thermopause. The altitude of the thermopause averages 700 km but varies with solar activity, ranging from about 500-1000 km. The temperature inversion is a result of absorption of highly energetic solar radiation. Temperatures are highly dependent on solar activity and can rise to 1500 oC, though the gas molecules are so far apart that temperature in the usual sense is not well defined.
Exosphere: The exosphere is the outermost layer of Earth's atmosphere, ranging from the thermopause, or exobase, to thousands of kilometers into space. It is mainly composed of hydrogen, helium and some heavier molecules such as nitrogen, oxygen and carbon dioxide closer to the exobase. The particle density is too low to behave as a gas. Temperatures are constant with height and are dependent on solar activity, ranging from about 500-2000 K.
The turbopause marks the altitude in Earth's atmosphere below which turbulent mixing dominates. The region below the turbopause is known as the homosphere, where the chemical constituents are well mixed and the composition of the atmosphere remains constant. The region above the turbopause is the heterosphere, where molecular diffusion dominates and the residual atmospheric gases sort into strata according to molecular mass. The turbopause lies near the mesopause at an altitude of roughly 110 km.
| Table 1 Molecular weights and assumed fractional- volume composition of sea-level dry air |
||
| Gas species | Molecular weight Mi (kg/kmol) |
Fractional volume Fi (dimensionless) |
| N2 | 28.0134 | 0.78084 |
| O2 | 31.9988 | 0.209476 |
| Ar | 39.948 | 0.00934 |
| CO2 | 44.00995 | 0.000314 |
| Ne | 20.183 | 0.00001818 |
| He | 4.0026 | 0.00000524 |
| Kr | 83.80 | 0.00000114 |
| Xe | 131.30 | 0.000000087 |
| CH4 | 16.04303 | 0.000002 |
| H2 | 2.01594 | 0.0000005 |
Basic Assumptions and Equations
Ideal Gas Law
The gases that make up a planetary atmosphere can be treated like ideal gases, meaning that they obey the ideal gas law (also called perfect gas law). The ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions. The common form of the ideal gas law is,
| (1) | P × V = n × R* × T |
where P is the absolute pressure of the gas (Pa), V is the volume of the gas (m3), n is the amount of gas (kmol), T is the absolute temperature of the gas (K), and R* is the universal gas constant (8314.4621 J/kmol-K).
Additional forms of the equation include,
| (2) | P = ρ × R* × T / M |
| (3) | P = N × R* × T / NA |
| (4) | P = N × k × T |
And from equations (2) and (3) we find,
| (5) | ρ = N × M / NA |
where ρ is the density of the gas (kg/m3), M is the mean molecular weight (kg/kmol), N is the total number density (m-3), NA is the Avagadro constant (6.0221413×1026 kmol-1), and k is the Boltzmann constant (1.3806488×10-23 J/K).
Note that in equations containing both R* and M, and where M is constant, we may sometimes substitute the specific gas constant R, where R = R*/M.
Hydrostatic Equation
The hydrostatic equation states that whenever there is no vertical motion, the difference in pressure dP between two levels dz is caused by the weight of the layer of air. Mathematically, this statement can be written as,
| (6) | dP = –ρ × g × dz |
where g is the height-dependent acceleration of gravity. The inverse-square law of gravitation provides an expression for g as a function of altitude,
| (7) | g = go × [ ro / (ro + z) ]2 |
where go is the sea-level value of the acceleration of gravity (9.80665 m/s2) and ro is the effective radius of Earth at a specific latitude.
Using equations (2) and (6), the hydrostatic equation can be written as,
| (8) | dP = –(P × M / (R* × T)) × g × dz |
Integrating from level z1 to level z2 results in the hypsometric equation,
| (9) | P2 = P1 × e [ –g × M / (R* × T) × (z2 – z1) ] |
If we define scale height H as follows,
| (10) | H = R* × T / (M × g) |
equation (9) then becomes,
| (11) | P2 = P1 × e [ –(z2 – z1) / H ] |
Geopotential Height
It has been customary in standard-atmosphere calculations to effectively eliminate the variable portion of the acceleration of gravity by the transformation of geometric height z to geopotential height h, thereby simplifying both integration of the hydrostatic equation and the resulting expression for computing pressure. The relationship between geometric and geopotential altitude depends upon the concept of gravity.
The unit of measurement of geopotential is the standard geopotential meter (m'), which represents the work done by lifting a unit mass 1 geometric meter through a region in which the acceleration of gravity is uniformly 9.80665 m/s2. The geopotential of any point with respect to mean sea level (assumed zero potential), expressed in geopotential meters, is called geopotential altitude. Therefore, geopotential altitude h is given by,
| (12) |
and is expressed in geopotential meters (m') when the unit geopotential go' is set equal to 9.80665 m2/(s2m'). With geopotential altitude defined as above, the differential may be expressed as,
| (13) | go' × dh = g × dz |
This expression is used in the hydrostatic equation to reduce the number of variables prior to its integration, thereby leading to an expression for computing pressure as a function of geopotential height.
The relationship between geopotential height h and geometric height z are given by the following expressions,
| (14) | h = ro × z / (ro + z) |
| (15) | z = ro × h / (ro – h) |
Molecular-Scale Temperature
The molecular-scale temperature TM at a point is defined as the product of the kinetic temperature T and the ratio M/Mo, where M is the molecular weight of air at that point, and Mo is the sea-level value of M. Analytically,
| (16) | TM = T × Mo / M |
The principle virtue of the parameter TM is that it combines the variable portion of M with the variable T into a single new variable, in a manner somewhat similar to the combining of the variable portion of g with z to form the new variable h. When both of these transformations are introduced into the hydrostatic equation, and when TM is expressed as a linear function of h, the resulting differential equation has an exact integral. Under these conditions, the computation of P versus h becomes a simple process not requiring numerical integration.
Hydrostatic equation in terms of h and TM
With geopotential height h and molecular-scale temperature TM defined, equations (10) and (11) are re-written as,
| (17) | H = R* × TM / (Mo × go') |
| (18) | P2 = P1 × e [ –(h2 – h1) / H ] |
Part I — Homosphere
Molecular Weight
In that part of the atmosphere below the turbopause, mixing is dominant and the effect of diffusion and photochemical processes upon mean molecular weight is negligible. In this region the fractional composition of each species is assumed to remain constant and mean molecular weight M remains constant at its sea-level value Mo.
Temperature
Traditionally, standard atmospheres have defined temperature as a linear function of height to eliminate the need for numerical integration in the computation of pressure versus height. The function TM versus h is expressed as a series of successive linear equations, the general form of which is,
| (19) | TM = TM,b + LM,b × (h – hb) |
where LM is the molecular-scale temperature gradient, also called lapse rate. The value of subscript b refers to each of the successive layers.
Let's consider an example:
| Table 2 The defined reference levels and gradients of the linearly segmented temperature-height profile from the surface to 50 geometric kilometers |
||
| Subscript b |
Geopotential height, hb (km') |
Molecular-scale temperature gradient, LM,b (K/km') |
| 0 | 0 | –6.0 |
| 1 | 12 | 0.0 |
| 2 | 24 | +2.0 |
| 3 | 50 | |
where we have three layers — h0 = 0 to h1 = 12 km, h1 = 12 km to h2 = 24 km, and h2 = 24 km to h3 = 50 km.
The value of TM,b for the first layer (b = 0) is equal to To, the sea-level value of T, since at this level M = Mo. With this value of TM,b defined, and the set of values of hb and the corresponding values of LM,b defined in Table 2, the function TM of h is completely defined from the surface to 50 km'.
Suppose we define To = 290 K, then for b =0 we have,
therefore,
We now calculate the value of TM,b for the second layer (b = 1),
For the second layer, we have
And for the third layer (b = 2), we have
Pressure
Within the region of homogeneity, two different equations are used for computing pressure, in which pressure is a function of geopotential altitude. One equation is for the case when LM,b for a particular layer is not equal to zero, and the other when the value LM,b is zero. The first of these two expressions is,
| (20) | P = Pb × [ TM,b / (TM,b + LM,b × (h – hb)) ] (go' × Mo/(R* × LM,b)) |
and the latter is,
| (21) | P = Pb × e [ –go' × Mo × (h – hb) / (R* × TM,b) ] |
In these equations go', Mo, and R* are each defined single-valued constants, while LM,b and hb are each defined multi-valued constants in accordance with the value of b. The quantity TM,b is a multi-valued constant dependent on LM,b and hb. The reference-level value of Pb for b = 0 is the defined sea-level value Po. Values of Pb are obtained from the application of the appropriate equation for the case when h = hb+1.
These two equations yield the pressure for any desired geopotential altitude from sea level to the maximum hb. Pressures for negative values of h may also be computed from the first equation when subscript b is zero.
Using the values given in Table 2, let's now consider an example.
First we define our single-valued constants:
Note that the unusual units of R* and go' is because we're expressing h in units of km' rather than m'.
For the first layer (b = 0) we have,
Since LM,0 is not equal to zero, we use equation (20),
For the second layer (b = 1) we have,
Since LM,1 is equal to zero, we use equation (21),
And for the third layer (b = 2) we have,
Mass Density
Having computed temperature and pressure, mass density can be found using the ideal gas law,
| (22) | ρ = P × Mo / (R* × TM) |
Speed of Sound
The speed of sound C is calculated using the equation,
| (23) | C = (γ × R* × TM / Mo)1/2 |
where γ is the specific heat ratio. Specific heat ratio is the ratio of constant-pressure to constant-volume specific heat, Cp/Cv. Specific heat is a function of temperature; however, the specific heats of elemental gases (such as N2, O2 and Ar) vary little with temperature. Since these gases dominate Earth's atmosphere, γ for air can be assumed constant, where γ = 1.400 (dimensionless).
Part II — Heterosphere
Molecular Weight
In that part of the atmosphere above the turbopause, mean molecular weight decreases with increasing altitude. Two processes are primarily responsible for this: the first is the dissociation of molecular oxygen, and the second is diffusive separation, which becomes increasingly important relative to mixing in this height region.
The mean molecular weight M of a mixture of gases is,
| (24) | M = Σ(ni × Mi) / Σni = Σ(Fi × Mi) |
| where | Fi = ni / Σni |
where ni and Mi are the number density and defined molecular weight, respectively, of the individual gas species. Alternatively, Fi is the fractional volume of the individual gas species.
Temperature
In the view of the necessity for computing individual density-altitude profiles for each atmospheric species in the heterosphere, the use of molecular-scale temperature TM becomes impractical, and in this region kinetic temperature T is used as a governing parameter. In addition, the use of a linearly segmented temperature-height function, with discontinuous first derivatives, is often terminated in favor of one in which the first derivative is continuous. Furthermore, geometric altitude replaces geopotential altitude as the argument of the temperature-height function.
The observed temperature-height profiles usually show large gradients in the lower thermosphere. At greater altitudes, the gradients decrease with increasing height to the exobase, where the temperature approaches as asymptote (usually referred to as the exospheric temperature T∞), which varies with solar activity, time of day, and several other parameters.
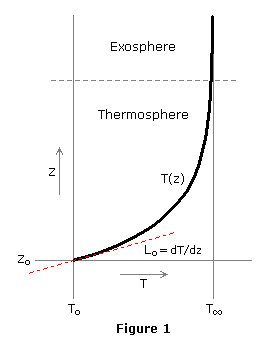 The temperature-altitude profile may be defined in terms of one or more successive functions. For example, the U.S. Standard Atmosphere, which we'll examine in detail later, uses three functions between 86 and 120 km — an isothermal layer, a layer in which T(z) has the form of an ellipse, and a constant positive gradient layer — and above 120 km, a layer in which T increases exponentially toward an asymptote.
The temperature-altitude profile may be defined in terms of one or more successive functions. For example, the U.S. Standard Atmosphere, which we'll examine in detail later, uses three functions between 86 and 120 km — an isothermal layer, a layer in which T(z) has the form of an ellipse, and a constant positive gradient layer — and above 120 km, a layer in which T increases exponentially toward an asymptote.
For the first of these functions, no one-size-fits-all instructions can be given, as the function(s) are selected on a case-by-case basis as needed to best fit the observed temperature-altitude profile in this region. The latter exponential function, however, is the predominate form at thermospheric altitudes. The standard exponential form is,
| (25) | T = T∞ – (T∞ – To) × EXP(–λξ) |
| where | λ = Lo / (T∞ – To) |
| ξ = (z – zo) × (ro + zo) / (ro + z) |
the principal features of which are shown in Figure 1. In this case, zo and To are the geometric altitude and kinetic temperature at the origin of the exponential function, and should not be confused with sea-level values, which typically carry the same denotation. Lo is the initial temperature gradient at the origin, and ro is the planet radius.
Pressure
Total pressure P is equal to the sum of the partial pressures for the individual species,
| (26) | P = ΣPi = Σni × k × T |
where k is the Boltzmann constant (1.3806488×10-23 J/K), T is T(z) as defined for the appropriate altitude regions, and Σni the sum of the number densities of the individual gas species comprising the atmosphere at altitude z. Neither ni, the number densities of individual species, nor Σni, the sum of the individual number densities, is known directly. Consequently, pressures cannot be computed without first determining ni for each of the significant species.
Mass Density
The total volumetric mass density is equal to,
| (27) | ρ = Σ(ni × Mi) / NA |
where ni and Mi are the number density and defined molecular weight of the individual gas species, and NA is the Avagadro constant (6.0221413×1026 kmol-1). As with pressure, densities cannot be computed without first determining ni for each of the significant species.
Number Densities
On Earth, in the altitude region between approximately 85 and 120 km, the effect of height- and time-dependent, molecular oxygen dissociation, and the competition between eddy and molecular diffusion combine to complicate the study of the height distribution of the atmospheric species, such that the generation of numerical values for the altitude profiles of physical parameters necessitates a considerable amount of numerical computation. More specifically, atomic oxygen becomes appreciable above 85 km, and diffusive separation begins to be effective at an average height of about 100 km. Also, in the regime where molecular diffusion becomes significant (above about 85 km), the effect of vertical winds in the composition in important.
These conditions lead to a complex dynamically oriented expression, applicable to each individual gas species, which includes vertical transport and diffusive separation. Ideally, this set of equations should be solved simultaneously, since the number densities of all the species are coupled through the expressions for molecular diffusion. Such a solution would require an inordinate amount of computation. A simpler approach is desired, which is found using some simplifying approximations, and by calculating the number densities of the individual species one at a time. Even this simpler approach is lengthier and more involved than we want to delve into here. However, if you wish to read more, refer to the following excerpt from NASA document SP-398:
Number Densities of Individual Species
Above approximately 120 km, it is relatively safe to assume that there is no further large-scale oxygen dissociation, and that diffusive equilibrium prevails. Under such conditions, the simultaneous equations governing molecular diffusion are no longer interdependent, and these equations can then be applied to each atmospheric constituent separately. In this case, the computation of the individual density-height profiles presents no greater difficulty than that of the total pressure or density below 80 km.
Number density decreases exponentially with height in an identical way to pressure. That is,
| (28) | nb+1 = nb × e[ –(zb+1 – zb) / H ] |
where the subscript b refers to successive atmospheric layers.
Referring to equation (10) we recall that scale height H is a function of molecular weight M, temperature T, and acceleration of gravity g. By computing n for each atmospheric constituent separately, M is constant and equal to the species' defined molecular weight. However, the function T(z) is height-dependent and non-linear, such as the function seen in equation (25). And now that z has replaced h as the parameter of height, g(z) is height-dependent acceleration of gravity, per equation (7). This leads to a complex and messy integration, which we'll not attempt to undertake.
Instead we can compute a table of values of n with sufficient accuracy if we select a table increment of height dz that is adequately small. Furthermore, we calculate n using the mean value of H for each atmospheric layer; that is, in equation (28) we use H = (Hb+Hb+1)/2. Using this averaging technique, dz = 1 km yields results that are likely adequate for our purposes, while anything smaller than dz = 0.1 km produces insignificant improvement.
The steps are as follows:
Now let's see an example...
Say we have molecular nitrogen with a number density of n0 = 3.73×1017 m-3 at a geometric altitude of z0 = 120 km. We want to compute n1 at an altitude of z1 = 121 km. The molecular weight of N2 is M = 28.0134 kg/kmol, the sea-level value of the acceleration of gravity is go = 9.80665 m/s2, the effective radius of Earth is ro = 6357 km, and assume that the function T(z) is defined.
At b = 0 we have,
At b = 1 we have,
Therefore, from equation (28),
The above steps are repeated for additional values of b and for the other atmospheric constituents (such as O2, O, Ar, He, and H). This will produce a table of values giving ni at regular height intervals for each individual species.
After computing values of ni, pressure and density are calculated using equations (26) and (27). If it is desired to compute pressure and density directly from geometric altitude, plot the values if lnP and lnρ versus z and fit a curve to the resulting data points. This yields functions lnP(z) and lnρ(z), from which we obtain P = EXP(lnP(z)) and ρ = EXP(lnρ(z)),
Speed of Sound
The limitations of the concept of speed of sound due to extreme attenuation are a concern at high altitudes. The attenuation that exists at sea level for high frequencies applies to successively lower frequencies as atmospheric pressure decreases, or as the mean free path increases. For this reason, the concept of speed if sound (except for frequencies approaching zero) progressively loses its range of applicability at high altitudes. Hence, speed of sound is generally not computed for high altitudes.
The World Meteorological Organization (WMO) has defined the Standard Atmosphere as follows:
"A hypothetical vertical distribution of atmospheric temperature, pressure and density which by international agreement and for historical reasons, is roughly representative of year-round, mid-latitude conditions. Typical usages are as a basis for pressure altimeter calibrations, aircraft performance calculations, aircraft and rocket design, ballistic tables and meteorological diagrams. Air is assumed to obey the perfect gas law and the hydrostatic equation which, taken together, relate temperature, pressure, and density with geopotential. Only one standard atmosphere should be specified at a particular time and this standard atmosphere must not be subjected to amendment except at intervals of many years."
Because of the interest of aerospace engineers and atmospheric scientists in conditions at much higher altitudes than those currently being considered by the WMO, members of the U.S. Committee on Extension to the Standard Atmosphere (COSEA) agreed to add the following paragraph to the above definition in describing the U.S. Standard Atmosphere, 1976, which extends to 1000 km:
"The atmosphere shall also be considered to rotate with the earth, and be an average over the diurnal cycle, semi-annual variation, and the range of conditions from active to quiet geomagnetic, and active to quiet sunspot conditions. Above the turbopause (about 110 km) generalized forms of the hydrostatic equations apply."
The U.S. Standard Atmosphere is an idealized, steady-state representation of mean annual conditions of Earth's atmosphere from the surface to 1000 km at latitude 45o N, as it is assumed to exist during a period with moderate solar activity. The defining meteorological elements are sea-level temperature and pressure, and a temperature-height profile to 1000 km. The air is assumed to be dry, and at heights sufficiently below 86 km, the atmosphere is assumed to be homogeneously mixed with a relative-volume composition leading to a constant mean molecular weight.
Adopted Constants
The following constants are adopted by this Standard for the purposes of computation. Note that the values of k, NA and R* differ from currently accepted values.
0 km to 86 km
For altitudes below 86 km, the U.S. Standard Atmosphere uses the method and equations described in the section Atmospheric Modeling, Part I – Homosphere. Values of hb and LM,b are given in Table 3. The reference-level values of TM,b and Pb for b = 0 are equal to the sea level values To = 288.15 K and Po = 101325 Pa.
| Table 3 The defined reference levels and gradients of the linearly segmented temperature-height profile from the surface to 86 geometric kilometers |
||
| Subscript b |
Geopotential height, hb (km') |
Molecular-scale temperature gradient, LM,b (K/km') |
| 0 | 0 | –6.5 |
| 1 | 11 | 0.0 |
| 2 | 20 | +1.0 |
| 3 | 32 | +2.8 |
| 4 | 47 | 0.0 |
| 5 | 51 | –2.8 |
| 6 | 71 | –2.0 |
| 7 | 84.8520 | |
The complete set of equations used to compute atmospheric properties from sea level to a geometric altitude of 86 km are summarized in Table 4. Be advised that the given altitudes are geopotential. In flight analysis or simulation, it is probable that you'll be working in geometric altitude. If this is the case, the geometric altitude z must be converted to geopotential altitude h using equation (14). Then, using the calculated value of h, the applicable equations are selected from Table 4 and the atmospheric properties are computed.
86 km to 1000 km
For altitudes above 86 km, the COSEA Task Group decided to include as constituents only those species that are known to contribute significantly to the total number density in any portion of the atmosphere between 86 km and 1000 km. Those gases that appear never to contribute more than about 0.5% of the total composition at any point within this height region, or which for various reasons do not exhibit predictable behavior, were purposely omitted. Using these guidelines, the following gases are included: N2, O, O2, Ar, and He. Atomic hydrogen is included at heights 150 km and above, but not included in boundary-value considerations at 86 km.
| Table 5 Number densities of various species at 86 km altitude |
|
| Species | Number density (m-3) |
| N2 | 1.129794 × 1020 |
| O | 8.600000 × 1016 |
| O2 | 3.030898 × 1019 |
| Ar | 1.351400 × 1018 |
| He | 7.581730 × 1014 |
Temperature
Below 80 km, where M is constant at Mo, T is equal to TM in accordance with equation (16). However, from Table 5 it is seen that the defined number densities at 86 km leads to a value of M = 28.9522 kg/kmol, about 0.04% less than Mo. To produce a smooth transition from this value of M to Mo, the altitude profile of M has arbitrarily been defined to decrease in terms of the ratio M/Mo from 1.000000 at 80 km to 0.9995788 at 86 km, thus the values of T correspondingly decrease from those of TM. At z7 = 86 km (h7 = 84.852 km') we find that TM,7 = 186.946 K and T7 = 186.8673 K.
At heights above 86 km, the temperature-altitude profile is defined in terms of four successive functions, each of which is specified in such a way that the first derivative of T with respect to z is continuous over the entire altitude region, 86 to 1000 km. These four functions begin successively at the first four base heights, zb listed in Table 6, and are designed to represent the following conditions: (1) an isothermal layer from 86 to 91 km; (2) a layer in which T(z) has the form of an ellipse from 91 to 110 km; (3) a constant, positive gradient layer from 110 to 120 km; and (4) a layer in which T increases exponentially toward an asymptote, as z increases from 120 to 1000 km.
| Table 6 The reference levels and function designations for each of the four segments of the temperature-height profile between 86 and 1000 km, with gradients specified for two linear segments, and with an intermediate reference height for the adopted atomic-hydrogen number-density value |
|||
| Subscript b |
Geometric height, zb (km) |
Kinetic- temperature gradient, LK,b (K/km) |
Form of function relating T to z |
| 7 | 86 | 0.0 | Linear |
| 8 | 91 | Elliptical | |
| 9 | 110 | 12.0 | Linear |
| 10 | 120 | Exponential | |
| 11 | 500 | ||
| 12 | 1000 | ||
For the layer from z7 = 86 km to z8 = 91 km, the temperature-altitude function is defined to be isothermally linear with respect to geometric altitude, so that the gradient of T with respect to z is zero (see Table 6). Thus, the standard form of the linear function degenerates to
Since T is defined to be constant for the entire layer, z7 to z8, the temperature at z8 is T8 = T7 = 186.8673 K, and the gradient at z8 is LK,8 = 0.0 K/km, the same as for LK,7.
For the layer from z8 = 91 km to z9 = 110 km, the temperature-altitude function is defined to be a segment of an ellipse expressed by
where Tc = 263.1905 K, A = –76.3232 K, a = –19.9429 km, and z is limited to values from 91 to 110 km. The equation is derived from the basic equation for an ellipse, to meet the values of T8 and LK,8 derived above, as well as defined values T9 = 240.0 K, and LK,9 = 12.0 K/km, for z9 = 110 km.
For the layer from z9 = 110 km to z10 = 120 km, T(z) has the standard form of the linear function, where subscript b is 9, such that Tb and LK,b are, respectively, the defined quantities T9 and LK,9, while z is limited to the range 110 to 120 km. Thus,
The value of T10 at z10 is found from the above to be 360.0 K.
For the layer from z10 = 120 km to z12 = 1000 km, T(z) is defined to have the exponential form of equation (25),
where
In the above expressions, T∞ is the exospheric temperature and equals the defined value 1000 K, which is assumed to represent mean solar conditions.
| Table 7 U.S. Standard Atmosphere, 86 to 1000 km |
|
|---|---|
| Geocentric Altitude, z (km) |
Kinetic Temperature, T (K) |
| 86-91 | 186.8673 |
| 91-110 | 263.1905 – 76.3232 × SQRT[1 – ((z – 91) / –19.9429)2] |
| 110-120 | 240 + 12 × (z – 110) |
| 120-1000 | 1000 – 640 × EXP(–0.01875 × ξ) where ξ = (z – 120) × (6356.766 + 120) / (6356.766 + z) |
Pressure and Density
From equations (26) and (27) we see that pressure and mass density in this height region are computed from the number densities of the individual gas species. However, we also learned that computation of number density, particularly between the altitudes of 86 km and 120 km, is a lengthier topic than we want to cover in this web page. Instead, we can obtain values of pressure and density from tables in the following document:
U.S. Standard Atmosphere, 1976
Using the tabulated data, we derive a set of equations from which we compute pressure and density for geometric altitudes from 86 km to 1000 km. The basic equation form is,
| (29) | EXP( A × z4 + B × z3 + C × z2 + D × z + E ) |
where the numerical value of the A through E coefficients are listed in Table 8.
| Table 8 U.S. Standard Atmosphere, 86 to 1000 km |
|||||||
|---|---|---|---|---|---|---|---|
| Geometric Altitude, z (km) |
Basic equation form: EXP( A × z4 + B × z3 + C × z2 + D × z + E ) |
||||||
| A | B | C | D | E | |||
| Pressure, P (Pa) | |||||||
| 86-91 | 0.000000 | 2.159582E-06 | –4.836957E-04 | –0.1425192 | 13.47530 | ||
| 91-100 | 0.000000 | 3.304895E-05 | –0.009062730 | 0.6516698 | –11.03037 | ||
| 100-110 | 0.000000 | 6.693926E-05 | –0.01945388 | 1.719080 | –47.75030 | ||
| 110-120 | 0.000000 | –6.539316E-05 | 0.02485568 | –3.223620 | 135.9355 | ||
| 120-150 | 2.283506E-07 | –1.343221E-04 | 0.02999016 | –3.055446 | 113.5764 | ||
| 150-200 | 1.209434E-08 | –9.692458E-06 | 0.003002041 | –0.4523015 | 19.19151 | ||
| 200-300 | 8.113942E-10 | –9.822568E-07 | 4.687616E-04 | –0.1231710 | 3.067409 | ||
| 300-500 | 9.814674E-11 | –1.654439E-07 | 1.148115E-04 | –0.05431334 | –2.011365 | ||
| 500-750 | –7.835161E-11 | 1.964589E-07 | –1.657213E-04 | 0.04305869 | –14.77132 | ||
| 750-1000 | 2.813255E-11 | –1.120689E-07 | 1.695568E-04 | –0.1188941 | 14.56718 | ||
| Density, ρ (kg/m3) | |||||||
| 86-91 | 0.000000 | –3.322622E-06 | 9.111460E-04 | –0.2609971 | 5.944694 | ||
| 91-100 | 0.000000 | 2.873405E-05 | –0.008492037 | 0.6541179 | –23.62010 | ||
| 100-110 | –1.240774E-05 | 0.005162063 | –0.8048342 | 55.55996 | –1443.338 | ||
| 110-120 | 0.00000 | –8.854164E-05 | 0.03373254 | –4.390837 | 176.5294 | ||
| 120-150 | 3.661771E-07 | –2.154344E-04 | 0.04809214 | –4.884744 | 172.3597 | ||
| 150-200 | 1.906032E-08 | –1.527799E-05 | 0.004724294 | –0.6992340 | 20.50921 | ||
| 200-300 | 1.199282E-09 | –1.451051E-06 | 6.910474E-04 | –0.1736220 | –5.321644 | ||
| 300-500 | 1.140564E-10 | –2.130756E-07 | 1.570762E-04 | –0.07029296 | –12.89844 | ||
| 500-750 | 8.105631E-12 | –2.358417E-09 | –2.635110E-06 | –0.01562608 | –20.02246 | ||
| 750-1000 | –3.701195E-12 | –8.608611E-09 | 5.118829E-05 | –0.06600998 | –6.137674 | ||
If lower accuracy can be tolerated, pressure and density can be computed using fewer equations that span larger altitude ranges. For instance, pressure and density over the entire 86 km to 120 km altitude range can be approximated using the following:
| (30) | P = EXP(–0.0000000422012 z5 + 0.0000213489 z4 – 0.00426388 z3 + 0.421404 z2 – 20.8270 z + 416.225 ) |
| (31) | ρ = EXP( 0.000000075691 z5 – 0.0000376113 z4 + 0.0074765 z3 – 0.743012 z2 + 36.7280 z – 729.346 ) |
While the coefficients in Table 8 will produce results that are generally accurate to about 4 digits, equations (30) and (31) are accurate to only 2 or 3 digits, though this may be good enough in some applications.
For situations where no particular date or location is specified, the U.S. Standard Atmosphere is a good representation of Earth's atmosphere, and an excellent model for flight simulations, or for other purposes where atmospheric properties vs. altitude must be known. However, there may be circumstances when a more specific model is needed or desired. The following are some alternative models.
Below 90 km
The Reference Atmospheres presented in this section were developed to provide Air Force engineers and designers of aerospace systems with up to date information on the seasonal, latitudinal, and longitudinal variations in the vertical distributions of the thermodynamics properties (pressure, temperature, and density) of the atmosphere in the Northern Hemisphere for altitudes up to 90 km. Special models are included to illustrate the magnitude of the changes in the vertical distributions of these atmospheric properties during extreme winter warmings and coolings of the stratosphere and mesosphere in artic and subarctic regions.The atmospheric models are defined by temperature-altitude profiles in which temperatures change linearly with respect to geopotential altitude. It is assumed that the air is dry, is in hydrostatic equilibrium, and behaves as a perfect gas. The molecular weight of air at sea level, 28.9644 kg/kmol, is assumed constant to 90 km. Actually, dissociation of molecular oxygen begins to take place near 80 km and molecular weight starts decreasing slowly with height. Consequently, the temperatures given in the tables for altitudes above 80 km are slightly but not significantly larger than the ambient kinetic temperature.
Numerical values for the various thermodynamic and physical constants used in computing the tables of atmospheric properties for these Reference Atmospheres are identical to those used in the preparation of the U.S. Standard Atmosphere, 1976, with two exceptions. Surface conditions for the atmospheres are based on mean monthly sea-level values of pressure and temperature for the appropriate latitude rather than on standard conditions. The accelerations of gravity at sea level for the latitudes were obtained from the following expression in which gravity g varies with latitude φ:
| (32) | gφ = 9.780356 × (1 + 0.0052885 × sin2 φ – 0.0000059 sin2 2φ) |
The relationship between geopotential altitude and geometric altitude is as expressed in equation (14).
| Table 9 Sea level acceleration of gravity and the effective radius of Earth for each latitude |
||
| Latitude φ |
Sea level gravity, gφ (m/s2) |
Effective Earth radius, ro (km) |
| 0 | 9.78036 | 6334.984 |
| 15 | 9.78381 | 6337.838 |
| 30 | 9.79324 | 6345.653 |
| 45 | 9.80665 | 6356.766 |
| 60 | 9.81911 | 6367.103 |
| 75 | 9.82860 | 6374.972 |
| 90 | 9.83208 | 6377.862 |
Sets of mean monthly Reference Atmospheres for altitudes up to 90 km have been developed for 15-degree intervals of latitude, including the equator and north pole, to provide information on the seasonal and latitudinal variations in the thermodynamic properties of the atmosphere. Properties of the January, April, July, and October models are presented in the following document:
Reference Atmospheres, 0 to 90 km
90 km to 110 km
These empirical atmospheres are based on a report entitled, "Atmospheric Structure and its Variation in the region from 25 to 120 km" by Groves (1971). In this section only the properties above 90 km are presented. The upper altitude of the models varies with latitude and time of year, depending on the availability of data. Above 90 km the data are primarily from rocketborne falling sphere, grenade and chemical release techniques. Data used are from all longitudes, with southern hemisphere data shifted by six months. Mean temperature values at latitudes from the equator to 70 degrees are given in Table 14-11 of the following document. Less accurate values (based on few data points) are indicated by an asterisk. Table 14-12 gives the corresponding pressure values and Table 14-13 the density values.
Reference Atmospheres, 90 to 110 km
120 km & Above
These atmospheres are based on a report by Jacchia (1971). Previous thermospheric models that assumed a single, constant set of boundary conditions at 120 km did not accurately represent variations in properties in the altitude region 120 to 180 km. To attempt to remedy this problem, Jacchia lowered the boundary to 90 km where it is known that there is an approximate isopycnic (constant density) layer, although the temperature shows important variations. In his models, all temperature profiles start from a constant value 183 K at 90 km. He did not include the model values below 110 km in order to disregard the less accurate region.
The following are the major types of variation of properties of the thermosphere:
The models described in this section include both long and short-term solar activity effects and diurnal, but not semi-diurnal, variations. Atmospheric response to storms is represented in terms of Kp, the 3-h geomagnetic planetary index. This provides reasonable representation of the response to most storms, but not all.
The average semi-annual variation is reasonably modeled, but it must be pointed out that the amplitude of this effect, whose cause is not completely understood, varies from year to year. The seasonal-latitudinal variations of the lower atmosphere are not modeled, except for an empirical expression for density but not temperature changes. Attempts have been made to model empirically some of the effects of large-scale circulation that primarily affect the composition of the thermosphere. Density and composition fluctuations caused by gravity waves are not modeled.
Tables in this section are given with the exospheric temperature T∞ as the defining parameter. To determine the exospheric temperature for a particular time and location the following equations are used. The temperature Tc is the global nighttime minimum of the exospheric temperature when Kp is zero.
| (33) | Tc = 379 + 3.24 × |
where F10.7 is the 10.7-cm solar flux in solar flux units (10-22 W/m2-Hz) and ![]() 10.7 is the mean F10.7 solar flux. Averaged over five solar cycles between the years 1954-2008,
10.7 is the mean F10.7 solar flux. Averaged over five solar cycles between the years 1954-2008, ![]() 10.7 has the historical value of 129 SFU.
10.7 has the historical value of 129 SFU.
The diurnal variation of the exospheric temperature can be represented by,
| (34.a) | TD = Tc × (1 + R × cosm η) |
| (34.b) | TN = Tc × (1 + R × sinm θ) |
where TD is the maximum daily temperature and TN is the minimum daily temperature. R is a coefficient with a value of approximately 0.3, and
| η = 1/2 × |φ – δo| | |
| θ = 1/2 × |φ + δo| |
where φ is the latitude and δo is the Sun's declination. A value of 2.2 can be used for m.
For Kp above zero the exospheric temperature is increased by,
| (35) | ΔT∞ = 28 × Kp + 0.08 × EXP(Kp) |
Kp indices range from 0 (very quiet) to 9 (extremely disturbed). During the ten-year period 1994-2013, Kp had a median value of 2.
The following document contains model values of kinetic temperature, logarithms of the concentrations of N2, O2, O, Ar, He, and H, mean molecular weight, and density as functions of altitude for exospheric temperatures ranging from 500 to 1600 K.
Reference Atmospheres, 120 to 2000 km
Overview
The atmosphere of Mars is similar to Earth's in that it is thin and relatively transparent to sunlight. Mars' spin rate and axial tilt are also Earthlike. Thus, the Martian atmosphere falls into the category of a rapidly rotating, differentially heated atmosphere with a solid lower boundary. However, there are also important differences. The Martian atmosphere is primarily carbon dioxide with a much lower surface pressure than Earth's (about 0.6% of Earth), and Mars does not have an Earthlike hydrological cycle.
The variation of temperature with height on Mars gives rise to a troposphere, a mesosphere, and a thermosphere. Mars does not have a stratosphere because it lacks an ozone layer. The tropopause on Mars is deep by comparison to Earth, extending to almost 60 km. In the Martian mesosphere, temperatures become nearly constant. In the thermosphere, temperatures increase because of heating due to the absorption of solar radiation. The base of the thermosphere is about 120 km. Mars, like Earth, has an isothermal exosphere, which begins at about 160 km to 250 km.
Mars is colder than Earth, experiences a much greater seasonal change in available insolation (40% compared to 6% for Earth), and has Earthlike diurnal and seasonal changes. The globally averaged surface temperature of Mars is approximately 215 K. However, because Mars lacks oceans, its surface temperatures undergo considerable seasonal, diurnal, and latitudinal variation. The lowest surface temperatures (~150 K) occur in polar regions during winter, the highest surface temperatures (~300 K) occur in the southern subtropics when Mars is closest to the Sun. In these same regions, diurnal variations can exceed 100 K.
| Table 10 Composition of the Martian lower atmosphere (< 120 km) |
|
| Gas species | Abundance |
| CO2 | 95.32% |
| N2 | 2.7% |
| Ar | 1.6% |
| O2 | 0.13% |
| CO | 0.08% |
| H2O | 210 ppm |
| NO | 100 ppm |
| Ne | 2.5 ppm |
| HDO | 0.85 ppm |
| Kr | 0.3 ppm |
| Xe | 0.08 ppm |
Atmospheric Model - Introduction
Although complex models of the Martian atmosphere exist, for this web page we'll produce our own model.
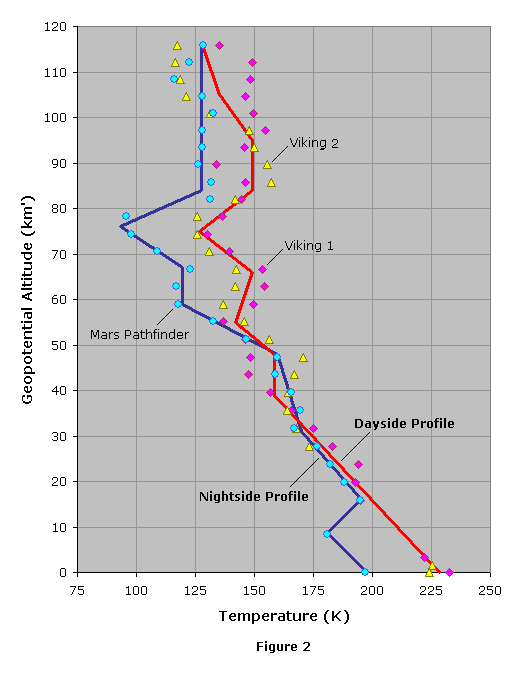
To date, all spacecraft that have landed on Mars have done so in either the equatorial region or the northern hemisphere. The first three landers to accomplish the feat – Viking 1, Viking 2, and Mars Pathfinder – touched down at northern latitudes during the summer season. There are a couple reasons for this: (1) landing near the equator, or at higher latitudes during the summer, provides the solar illumination needed for the operation of solar cells and the production of electricity; and (2) most of the northern hemisphere, and some of the equatorial regions, are of generally lower elevation than the southern hemisphere, thus allowing a lander to descend into a deeper and denser atmosphere, greatly improving the effectiveness of parachutes.
Since the Viking and Pathfinder missions are representative of the sites that most spacecraft are likely to land, we can use data from these missions to construct our model. Atmospheric data from the Viking missions can be found here in tabular form, and data from Pathfinder can be found here in graphical form. It is unclear how the reported altitudes are measured, though the following assumptions are made: (1) Viking altitudes from 0 to 4.5 km are measured from the ground surface, and (2) all other altitudes are geometric height above the zero-datum.
While Viking 1 (afternoon) and Viking 2 (morning) both landed during the daytime, Pathfinder landed at night near what is typically the coldest time of the day. Because of this, the Pathfinder data differs from that of Viking, leading us to construct two models. One model will be based on an average of the Viking 1 and Viking 2 data to give us a dayside model, while the other will be based on Pathfinder to give us a nightside model.
Using the Viking data we can compute the mean molecular weight using equation (2), from which we find a slight decrease in molecular weight starting at about 120 km altitude. We also see that there are some gaps in the spacecraft data above this altitude. A geometric altitude of 120 km, therefore, appears to be an ideal height to terminate the first of our models. The data is most complete in this range and we can consider the atmosphere to be a homogenous mixture of gases with a constant molecular weight.
Below 120 km, our models will employ the same method and equations as described in the section Atmospheric Modeling, Part I – Homosphere.
Adopted Constants
The following constants are adopted for the purposes of computation.
Since Mars has no oceans, the term "sea level" has no meaning. We must, therefore, define some other arbitrary zero-elevation level or datum for mapping the surface. The datum for Mars is arbitrarily defined in terms of a constant atmospheric pressure, which has been chosen as 610.5 Pa, on the basis that below this pressure liquid water can never be stable. That is, the value of Po is defined as 610.5 Pa.
For the value of ro we select Mars' volumetric radius, which is derived from an equatorial radius of 3396.19 km and a polar radius of 3376.20 km. This value of ro corresponds to a geocentric latitude of 35.2 degrees on the reference ellipsoid, which is ideal as this is midway between the latitudes of the two Viking landers. The datum-level acceleration of gravity go is calculated for this latitude and takes into account both gravitational attraction and centrifugal force.
0 km to 120 km
The first step is to develop temperature-height profiles for our dayside and nightside models. After converting the given values of z to h, we plot h versus TM for Viking 1, Viking 2 and Mars Pathfinder. We then look for a series of line segments that best fits the data points. To minimize the number of line segments, we try to match general patterns in the data rather than trying to account for every observed change in gradient. We decide on the following, where each temperature-height profile consists of nine line segments.
Tables 11 and 12 give the reference levels and gradients for our two temperature-height profiles. The reference-level value of Pb at b = 0 is the defined value Po = 610.5 Pa, while the values of TM,b at b = 0 are found to be 228.5 K for the dayside and 198.0 K for the nightside.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Given the above set of values and definitions, the functions TM(h) and P(h) are completely defined from the surface to a geometric altitude of 120 km (see Table 13).
Since the atmosphere of Mars consists predominately of carbon dioxide, the specific heat ratio of Martian air is much more sensitive to changes in temperature than air on Earth. For altitudes below 120 km, a good approximation of γ can be found using,
| (36) | γ = 0.000001409 TM2 – 0.001192 TM + 1.5175 |
Also note that since Mars has no oceans to fill its lowest elevations, there are large areas of the surface that lie below the vertical datum. It is not unusual for a spacecraft to land at a site that has a surface elevation of –2, –3 or even –4 km, which should be considered in any simulation.
| Table 13 Model of Martian Atmosphere, 0 to 120 km |
|||
|---|---|---|---|
| Geopotential Altitude, h (km') |
Molecular-Scale Temperature, TM (K) |
Pressure, P (Pa) |
|
| Dayside : Summer : 20-50oN | |||
| (–8)-39 | 228.50 – 1.80 × h | 610.5 × [228.50 / (228.50 – 1.80 × h)] (19.435 / –1.80) | |
| 39-48 | 158.30 | 11.6025 × EXP[–19.435 × (h – 39) / 158.30] | |
| 48-55 | 271.10 – 2.35 × h | 3.84305 × [158.30 / (158.30 – 2.35 × (h – 48))] (19.435 / –2.35) | |
| 55-66 | 106.10 + 0.65 × h | 1.55091 × [141.85 / (141.85 + 0.65 × (h – 55))] (19.435 / 0.65) | |
| 66-75 | 314.00 – 2.50 × h | 0.356464 × [149.00 / (149.00 – 2.50 × (h – 66))] (19.435 / –2.50) | |
| 75-84 | –61.00 + 2.50 × h | 0.0998430 × [126.50 / (126.50 + 2.50 × (h – 75))] (19.435 / 2.50) | |
| 84-95 | 149.00 | 0.0279653 × EXP[–19.435 × (h – 84) / 149.00] | |
| 95-105 | 282.00 – 1.40 × h | 0.00666032 × [149.00 / (149.00 – 1.40 × (h – 95))] (19.435 / –1.40) | |
| 105-115.897 | 203.25 – 0.65 × h | 0.00169282 × [135.00 / (135.00 – 0.65 × (h – 105))] (19.435 / –0.65) | |
| Nightside : Summer : 20oN | |||
| (–8)-8.5 | 198.00 – 2.00 × h | 610.5 × [198.00 / (198.00 – 2.00 × h)] (19.435 / –2.00) | |
| 8.5-16 | 164.85 + 1.90 × h | 255.172 × [181.00 / (181.00 + 1.90 × (h – 8.5))] (19.435 / 1.90) | |
| 16-31 | 222.45 – 1.70 × h | 117.537 × [195.25 / (195.25 – 1.70 × (h – 16))] (19.435 / – 1.70) | |
| 31-48 | 188.35 – 0.60 × h | 23.7302 × [169.75 / (169.75 – 0.60 × (h – 31))] (19.435 / –0.60) | |
| 48-59 | 334.75 – 3.65 × h | 3.18820 × [159.55 / (159.55 – 3.65 × (h – 48))] (19.435 / –3.65) | |
| 59-67 | 119.40 | 0.681102 × EXP[–19.435 × (h – 59) / 119.40] | |
| 67-76 | 313.70 – 2.90 × h | 0.185218 × [119.40 / (119.40 – 2.90 × (h – 67))] (19.435 / –2.90) | |
| 76-84 | –233.50 + 4.30 × h | 0.0354632 × [93.30 / (93.30 + 4.30 × (h – 76))] (19.435 / 4.30) | |
| 84-115.897 | 127.70 | 0.00858406 × EXP[–19.435 × (h – 84) / 127.70] | |
| Density, ρ (kg/m3) = P/(RTM) Speed of sound, C (m/s) = (γRTM)1/2 Specific gas constant, R = 191.181 J/kg-K Specific heat ratio, γ = 0.000001409 TM2 – 0.001192 TM + 1.5175 |
|||
120 km to 300 km
The only in situ measurements of Mars' upper atmosphere come from the Viking 1 and Viking 2 mission descents in 1976. Neutral mass spectrometers carried on the aeroshells of Viking 1 and 2 indicate that carbon dioxide is the major constituent of the Martian atmosphere in the altitude range of 120 to 200 km. The atmosphere contains detectable concentrations of nitrogen, argon, carbon monoxide, molecular oxygen, atomic oxygen, and nitric oxide. The Viking measurements are shown in Figure 3, with scale height extrapolations to 300 km.
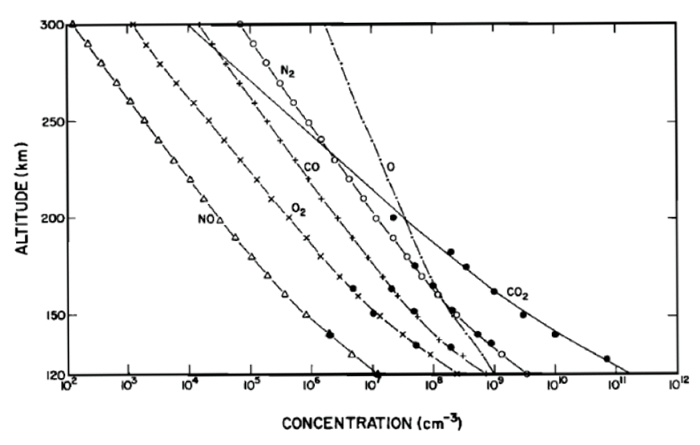
| Figure 3 — Upper thermospheric fits of the neutral measurements made by Viking 1 & 2 descent missions in 1976 (extended to 300 km) [Source: Hanson et al. 1977]. |
Since our previous "dayside" model is also based on measurements from Viking 1 and 2, we can match the dayside model to the data in Figure 3 to create one complete model that extends from the surface to an altitude of 300 km.
First, we use the equations in Table 13 to compute the boundary-level conditions at a geometric altitude of 120 km (h9 = 115.897 km'),
From Figure 3 we estimate the fractional volume Fi of the individual gas species at 120 km. Using equation (24) we compute the mean molecular weight M of the gas mixture, then the total number density N using equation (5). Finally, the number density ni of each gas species is found by ni = Fi × N.
| Table 14 Molecular weight, fractional volume composition, and number densities of various species at 120 km altitude |
|||
| Species | Mi (kg/kmol) | Fi | ni (m-3) |
| CO2 | 44.00995 | 0.96850 | 1.8550×1017 |
| N2 | 28.0134 | 0.01990 | 3.8116×1015 |
| O | 15.9994 | 0.00585 | 1.1205×1015 |
| CO | 28.0101 | 0.00425 | 8.1404×1014 |
| O2 | 31.9988 | 0.00143 | 2.7390×1014 |
| NO | 30.0061 | 0.00007 | 1.3408×1013 |
| M = 43.4416 | N = 1.9154×1017 | ||
Having defined the number densities at the boundary-level, we now need the temperature-height profile for altitudes over 120 km. We first we notice that the mean molecular weight at 120 km, M = 43.4416 kg/kmol, is slightly less than our defined surface level value of Mo = 43.49 kg/kmol. Therefore, at z9 = 120 km we find that T9 = 127.775 K.
Figure 4 compares day and night temperature profiles, as well as their variations with time. Present and past Martian thermospheres see their natural temperature increase with altitude first, and then become isothermal above some level. This level is reached at lower altitudes at night compared to day (dashed versus solid lines), and at present to past. Neutral thermospheric temperatures are found to be higher in the past.
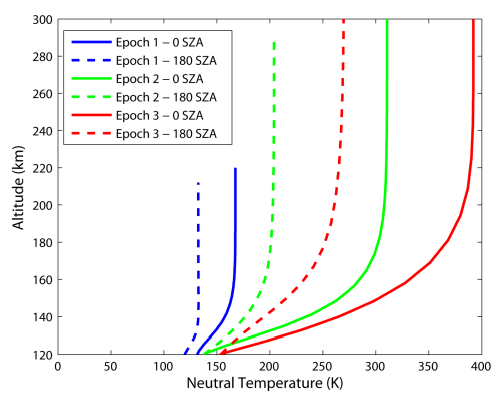
| Figure 4 — Profile of the neutral temperature in the Martian upper thermosphere (120 to 300 km altitude) at the equatorial noon (0o SZA) for epoch 1, 2 and 3 (blue, green and red lines, respectively) for low solar conditions. |
From Figure 4 we see that the temperature of the Martian thermosphere takes the exponential form of equation (25),
While ro, z9 and T9 are defined, T∞ and λ are as yet unknown.
To generate a model that replicates as closely as possible the number densities shown in Figure 3, it is found by trial and error that best results are obtained when,
With the information now at hand, we use the method described in the section Atmospheric Modeling, Part II – Heterosphere to compute the number densities of gas species in the Martian upper atmosphere. Since Figures 3 and 4 terminate at 300 km, we'll also stop at this altitude. The resulting equations are summarized in Table 15. Actual atmospheric conditions vary considerably depending on spatial, seasonal and solar cycle factors.
| Table 15 Model of Martian Atmosphere, 120 to 300 km |
|
|---|---|
| Geocentric Altitude, z (km) |
Functions: T(z), P(z) and ρ(z) |
| Temperature (K) | |
| 120-300 | 200 – 72.225 × EXP(–0.0195 × ξ) where ξ = (z – 120) × (3389.51 + 120) / (3389.51 + z) |
| Pressure (Pa) | |
| 120-200 | EXP( –4.18520E-10 z5 + 3.45846E-07 z4 – 1.13352E-04 z3 + 0.0188613 z2 – 1.71718 z + 61.10381 ) |
| 200-300 | EXP( –4.83452E-11 z5 + 6.96178E-08 z4 – 4.03197E-05 z3 + 0.0117655 z2 – 1.76494 z + 93.67154 ) |
| Density (kg/m3) | |
| 120-200 | EXP( –2.55314E-10 z5 + 2.31927E-07 z4 – 8.33206E-05 z3 + 0.0151947 z2 – 1.52799 z + 48.69659 ) |
| 200-300 | EXP( 2.65472E-11 z5 – 2.45558E-08 z4 + 6.31410E-06 z3 + 4.73359E-04 z2 – 0.443712 z + 23.79408 ) |
Overview
Although Venus is quite similar to Earth in size and distance from the Sun, its atmosphere is strikingly different from Earth's. The atmosphere of Venus is much more massive, with a total mass 93 times that of Earth, and is composed primarily of carbon dioxide, along with some nitrogen and other trace gases. A hydrosphere is absent on Venus — there is a very low abundance of water in any form. These compositional differences point to a drastically different evolution of the Venusian and terrestrial atmospheres through geological history.
The current state of the Venusian atmosphere also shows great differences from that of Earth. There is a strong greenhouse effect that raises the surface temperature to about 735 K, despite the fact that cloud cover strongly reflects sunlight so that less heat flux is absorbed on Venus than on Earth. The Venusian clouds are featureless and opaque in the visible. The clouds are composed of droplets of sulfuric acid, produced by photochemistry in the upper atmosphere.
The solid body of Venus rotates very slowly, with a period of 243 days, in the opposite direction to the general rotation of the solar system. The general circulation of the Venus atmosphere is dominated by rotation of the atmosphere in the same direction as that of the solid planet but increasing in speed with height from the surface up to the cloud tops. It reaches maximum speed (~100 m/s) near the cloud tops, where the rotation period is about 4 days. Atmospheric dynamics are thus very different on Venus than on Earth.
The length of a solar day on Venus is 116.75 Earth days. In spite of this long time, there is very little day-night temperature contrast in the lower atmosphere. There is also very little latitudinal temperature contrast in the lower atmosphere of Venus. Within the clouds, however, there is a latitudinal temperature gradient, cooler toward the poles by about 20 K. At higher altitude the temperature gradient reverses.
The temperature-height profile of Venus gives rise to a troposphere, a mesosphere, and a thermosphere. The troposphere, which contains about 99% of the atmosphere by mass, begins at the surface and extends upwards to about 65 km. The mesosphere of Venus extends from about 65 km to 120 km in altitude, and the thermosphere begins at around 120 km, eventually reaching the upper limit of the atmosphere (exosphere) at about 220 km to 350 km.
| Table 16 Composition of the Venusian lower atmosphere (< 100 km) |
|
| Gas species | Abundance |
| CO2 | 96.5% |
| N2 | 3.5% |
| SO2 | 150 ppm |
| Ar | 70 ppm |
| H2O | 20 ppm |
| CO | 17 ppm |
| He | 12 ppm |
| Ne | 7 ppm |
Atmospheric Model - Introduction
The temperature of Venus' lower atmosphere varies little globally, therefore we can make due with a single model of this height region. The temperature-height profile for 0 km to 100 km will be based on the tabulated values found here. The data are based on measurements made by Pioneer Venus mission's atmospheric probes and other spacecraft.
At higher altitudes there is significant diurnal variation, however a model of the mean atmosphere will suit many of our needs. For example, a spacecraft in a low circular orbit will repeatedly cycle through day and night conditions, thus the total effect of the atmosphere can be predicted using a mean model.
For altitudes over 100 km, we will base our equations on the atmospheric model of Bougher et al., 1986.
Adopted Constants
The following constants are adopted for the purposes of computation.
Since the Venus' period of rotation is so slow (243 days), there is insignificant polar flattening and centrifugal forces. We can, therefore, consider go and ro constant across the globe.
0 km to 100 km
From the previously referenced table of geometric height and temperature, we estimate a series of line segments to describe the temperature-geopotential height profile. The selected reference levels and gradients are given in Table 17. The values of LM,4 and LM,5 are selected so that the computed properties at the 100 km boundary level exactly match those of the Bougher et al. model. The reference-level values of TM,b and Pb at b = 0 are the defined values To = 735 K and Po = 9,332,000 Pa.
| Table 17 The defined reference levels and gradients of the linearly segmented temperature-height profile from the surface to 100 geometric kilometers |
||
| Subscript b |
Geopotential height, hb (km') |
Molecular-scale temperature gradient, LM,b (K/km') |
| 0 | 0 | –7.63 |
| 1 | 15.5 | –8.47 |
| 2 | 36.5 | –6.91 |
| 3 | 49.5 | –9.72 |
| 4 | 58 | –3.27687 |
| 5 | 87 | –0.499214 |
| 6 | 98.3745 | |
Given the above set of values and definitions, the functions TM(h) and P(h) are completely defined from the surface to a geometric altitude of 100 km (see Table 18).
Like Mars, the high carbon dioxide content of the Venusian atmosphere results in the specific heat ratio γ being highly dependent on temperature. For altitudes below 100 km, the value of γ is estimated using,
| (37) | γ = –8.175E-10 TM3 + 0.000001665 TM2 – 0.001233 TM + 1.5336 |
| Table 18 Model of Venusian Atmosphere, 0 to 100 km |
|||
|---|---|---|---|
| Geopotential Altitude, h (km') |
Molecular-Scale Temperature, TM (K) |
Pressure, P (Pa) |
|
| (–3)-15.5 | 735.00 – 7.63 × h | 9332000 × [735.000 / (735.000 – 7.63 × h)] (46.353 / –7.63) | |
| 15.5-36.5 | 748.02 – 8.47 × h | 3214540 × [616.735 / (616.735 – 8.47 × (h – 15.5))] (46.353 / –8.47) | |
| 36.5-49.5 | 691.08 – 6.91 × h | 499392 × [438.865 / (438.865 – 6.91 × (h – 36.5))] (46.353 / –6.91) | |
| 49.5-58 | 830.175 – 9.72 × h | 107458 × [349.035 / (349.035 – 9.72 × (h – 49.5))] (46.353 / –9.72) | |
| 58-87 | 456.4735 – 3.27687 × h | 29634.9 × [266.415 / (266.415 – 3.27687 × (h – 58))] (46.353 / –3.27687) | |
| 87-98.3745 | 214.8174 – 0.499214 × h | 57.7754 × [171.386 / (171.386 – 0.499214 × (h – 87))] (46.353 / –0.499214) | |
| Density, ρ (kg/m3) = P/(RTM) Speed of sound, C (m/s) = (γRTM)1/2 Specific gas constant, R = 191.357 J/kg-K Specific heat ratio, γ = –8.175E-10 TM3 + 0.000001665 TM2 – 0.001233 TM + 1.5336 |
|||
100 km to 300 km
Using the equations in Table 18, we find the boundary-level conditions at a geometric altitude of 100 km (h6 = 98.3745 km'),
Above 100 km, our model is based on that of Bougher et al., 1986. The Bougher model gives values of scale height, total number density, relative number densities (fractional volume) of O and CO, and temperature, at intervals of 5 km for five different values of solar zenith angle (SZA), ranging from 0o (noon) to 180o (midnight). Our model will average the values of the five SZA to give a global mean. Although values for SZA = 0o extend to an altitude of 210 km, the others stop short of this height. The first thing we want to do is extrapolate all sets of values to an altitude of 210 km.
To do this we need to know the number densities of the individual atmospheric constituents. We're given the total number density N and the fractional volume of O and CO. We can assume the balance of the atmosphere consists of CO2 and N2 in some unknown proportion. If the mean molecular weight at some point is known, we can compute the required fractional volumes of CO2 and N2 at that point. Since H and T are given, and g is a function of altitude, using equation 10 we can compute M. We then have,
With two equations and two unknowns, we calculate the fractional volumes of CO2 and N2. With all values of Fi now known, the number densities of the individual species are found using ni = Fi × N.
Using the method described in the section Atmospheric Modeling, Part II – Heterosphere, we extrapolate all the Bougher et al. data sets to an altitude of 210 km. We then average the number densities and temperature for each interval of height. Table 19, for example, gives the mean abundance of each species at the boundary-level altitude of 100 km. The average value of T at 100 km is 161.860 K.
| Table 19 Molecular weight, fractional volume composition, and number densities of various species at 100 km altitude |
|||
| Species | Mi (kg/kmol) | Fi | ni (m-3) |
| CO2 | 44.00995 | 0.902050 | 1.02112×1021 |
| N2 | 28.0134 | 0.096996 | 1.0980×1020 |
| CO | 28.0101 | 0.000793 | 8.9780×1017 |
| O | 15.9994 | 0.000161 | 1.8200×1017 |
| M = 42.4412 | N = 1.1320×1021 | ||
From Table 19 we see that M < Mo. Recalling that TM,6 = 165.7075 K and using equation (16), we find that T6 = 161.860 K, which matches the average of the Bougher et al. values for that height. Given T6 and the values in Table 19, and using equations (4) and (5), we find that the computed values of P6 and ρ6 match those previously computed using the equations in Table 18, thereby confirming we have a smooth transition at z6 = 100 km.
The average values of number density and temperature derived from the Bougher et al. model extend to an altitude of 210 km. The 210 km values are extrapolated further to an altitude of 300 km to cover a wider range of potential orbits. We extrapolate no further because we're getting into an unknown region. It is certain that lighter species (helium and hydrogen), which were ignored at low altitude, are found in greater proportion at high altitudes.
It is found that temperature above an altitude of 150 km follows the basic exponential form of equation (25). Between 100 km and 150 km, temperature is computed using a series of polynomials fitted to the tabulated values of temperature. Likewise, equations for pressure and temperature are derived from tabulated values.
| Table 20 Model of Venusian Atmosphere, 100 to 300 km |
|
|---|---|
| Geocentric Altitude, z (km) |
Functions: T(z), P(z) and ρ(z) |
| Temperature (K) | |
| 100-115 | –0.00504 z3 + 1.6112 z2 – 171.678 z + 6257.66 |
| 115-135 | 0.00001733333 z4 – 0.007826667 z3 + 1.375967 z2 – 112.72633 z + 3795.74 |
| 135-150 | –0.00472 z3 + 1.9952 z2 – 278.41 z + 12991.22 |
| 150-300 | 208.21 – 16.49 × EXP(–0.106428 × ξ) where ξ = (z – 150) × (6051.8 + 150) / (6051.8 + z) |
| Pressure (Pa) | |
| 100-140 | EXP( 1.255723E-06 z4 – 5.579211E-04 z3 + 0.09250745 z2 – 7.058415 z + 214.0424 ) |
| 140-210 | EXP( –1.884212E-09 z5 + 1.784462E-06 z4 – 6.803835E-04 z3 + 0.1308837 z2 – 12.79816 z + 499.6816 ) |
| 210-300 | EXP( 4.489586E-09 z4 – 4.899145E-06 z3 + 0.002015526 z2 – 0.4456979 z + 25.26467 ) |
| Density (kg/m3) | |
| 100-140 | EXP( 9.776973E-07 z4 – 4.431351E-04 z3 + 0.07498141 z2 – 5.886184 z + 174.7343 ) |
| 140-210 | EXP( –2.869772E-09 z5 + 2.658564E-06 z4 – 9.897302E-04 z3 + 0.1856624 z2 – 17.67973 z + 664.9583 ) |
| 210-300 | EXP( 9.249815E-09 z4 – 1.006456E-05 z3 + 0.004115272 z2 – 0.8247589 z + 39.32464 ) |
Compiled, edited and written in part by Robert A. Braeunig, 2014.
Bibliography