 |
ROCKET PROPULSION |
 |
ROCKET PROPULSION |
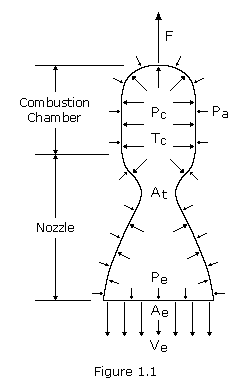 Thrust is the force that propels a rocket or spacecraft and is measured in pounds, kilograms or Newtons. Physically speaking, it is the result of pressure which is exerted on the wall of the combustion chamber.
Thrust is the force that propels a rocket or spacecraft and is measured in pounds, kilograms or Newtons. Physically speaking, it is the result of pressure which is exerted on the wall of the combustion chamber.
Figure 1.1 shows a combustion chamber with an opening, the nozzle, through which gas can escape. The pressure distribution within the chamber is asymmetric; that is, inside the chamber the pressure varies little, but near the nozzle it decreases somewhat. The force due to gas pressure on the bottom of the chamber is not compensated for from the outside. The resultant force F due to the internal and external pressure difference, the thrust, is opposite to the direction of the gas jet. It pushes the chamber upwards.
To create high speed exhaust gases, the necessary high temperatures and pressures of combustion are obtained by using a very energetic fuel and by having the molecular weight of the exhaust gases as low as possible. It is also necessary to reduce the pressure of the gas as much as possible inside the nozzle by creating a large section ratio. The section ratio, or expansion ratio, is defined as the area of the exit Ae divided by the area of the throat At.
The thrust F is the resultant of the forces due to the pressures exerted on the inner and outer walls by the combustion gases and the surrounding atmosphere, taking the boundary between the inner and outer surfaces as the cross section of the exit of the nozzle. As we shall see in the next section, applying the principle of the conservation of momentum gives
![]()
where q is the rate of the ejected mass flow, Pa the pressure of the ambient atmosphere, Pe the pressure of the exhaust gases and Ve their ejection speed. Thrust is specified either at sea level or in a vacuum.
The linear momentum (p), or simply momentum, of a particle is the product of its mass and its velocity. That is,
![]()
Newton expressed his second law of motion in terms of momentum, which can be stated as "the resultant of the forces acting on a particle is equal to the rate of change of the linear momentum of the particle". In symbolic form this becomes
![]()
which is equivalent to the expression F=ma.
If we have a system of particles, the total momentum P of the system is the sum of the momenta of the individual particles. When the resultant external force acting on a system is zero, the total linear momentum of the system remains constant. This is called the principle of conservation of linear momentum. Let's now see how this principle is applied to rocket mechanics.
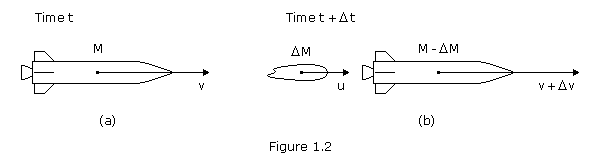
Consider a rocket drifting in gravity free space. The rocket's engine is fired for time ![]() t and, during this period, ejects gases at a constant rate and at a constant speed relative to the rocket (exhaust velocity). Assume there are no external forces, such as gravity or air resistance.
t and, during this period, ejects gases at a constant rate and at a constant speed relative to the rocket (exhaust velocity). Assume there are no external forces, such as gravity or air resistance.
Figure 1.2(a) shows the situation at time t. The rocket and fuel have a total mass M and the combination is moving with velocity v as seen from a particular frame of reference. At a time ![]() t later the configuration has changed to that shown in Figure 1.2(b). A mass
t later the configuration has changed to that shown in Figure 1.2(b). A mass ![]() M has been ejected from the rocket and is moving with velocity u as seen by the observer. The rocket is reduced to mass M-
M has been ejected from the rocket and is moving with velocity u as seen by the observer. The rocket is reduced to mass M-![]() M and the velocity v of the rocket is changed to v+
M and the velocity v of the rocket is changed to v+![]() v.
v.
Because there are no external forces, dP/dt=0. We can write, for the time interval ![]() t
t
![]()
where P2 is the final system momentum, Figure 1.2(b), and P1 is the initial system momentum, Figure 1.2(a). We write
![]()
If we let ![]() t approach zero,
t approach zero, ![]() v/
v/![]() t approaches dv/dt, the acceleration of the body. The quantity
t approaches dv/dt, the acceleration of the body. The quantity ![]() M is the mass ejected in
M is the mass ejected in ![]() t; this leads to a decrease in the mass M of the original body. Since dM/dt, the change in mass of the body with time, is negative in this case, in the limit the quantity
t; this leads to a decrease in the mass M of the original body. Since dM/dt, the change in mass of the body with time, is negative in this case, in the limit the quantity ![]() M/
M/![]() t is replaced by -dM/dt. The quantity u-(v+
t is replaced by -dM/dt. The quantity u-(v+![]() v) is Vrel, the relative velocity of the ejected mass with respect to the rocket. With these changes, equation (1.4) can be written as
v) is Vrel, the relative velocity of the ejected mass with respect to the rocket. With these changes, equation (1.4) can be written as
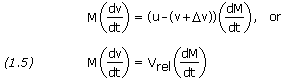
The right-hand term depends on the characteristics of the rocket and, like the left-hand term, has the dimensions of a force. This force is called the thrust, and is the reaction force exerted on the rocket by the mass that leaves it. The rocket designer can make the thrust as large as possible by designing the rocket to eject mass as rapidly as possible (dM/dt large) and with the highest possible relative speed (Vrel large).
In rocketry, the basic thrust equation is written as
![]()
where q is the rate of the ejected mass flow, Ve is the exhaust gas ejection speed, Pe is the pressure of the exhaust gases at the nozzle exit, Pa is the pressure of the ambient atmosphere, and Ae is the area of the nozzle exit. The product qVe, which we derived above (Vrel × dM/dt), is called the momentum, or velocity, thrust. The product (Pe-Pa)Ae, called the pressure thrust, is the result of unbalanced pressure forces at the nozzle exit. As we shall see latter, maximum thrust occurs when Pe=Pa.
Equation (1.6) may be simplified by the definition of an effective exhaust gas velocity, C, defined as
![]()
Equation (1.6) then reduces to
![]()
In the preceding section we saw that Newton's second law may be expressed in the form
![]()
Multiplying both sides by dt and integrating from a time t1 to a time t2, we write
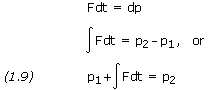
The integral is a vector known as the linear impulse, or simply the impulse, of the force F during the time interval considered. The equation expresses that, when a particle is acted upon by a force F during a given time interval, the final momentum p2 of the particle may be obtained by adding its initial momentum p1 and the impulse of the force F during the interval of time.
When several forces act on a particle, the impulse of each of the forces must be considered. When a problem involves a system of particles, we may add vectorially the momenta of all the particles and the impulses of all the forces involved. When can then write
![]()
For a time interval ![]() t, we may write equation (1.10) in the form
t, we may write equation (1.10) in the form
![]()
Let us now see how we can apply the principle of impulse and momentum to rocket mechanics.
Consider a rocket of initial mass M which it launched vertically at time t=0. The fuel is consumed at a constant rate q and is expelled at a constant speed Ve relative to the rocket. At time t, the mass of the rocket shell and remaining fuel is M-qt, and the velocity is v. During the time interval ![]() t, a mass of fuel q
t, a mass of fuel q![]() t is expelled. Denoting by u the absolute velocity of the expelled fuel, we apply the principle of impulse and momentum between time t and time t+
t is expelled. Denoting by u the absolute velocity of the expelled fuel, we apply the principle of impulse and momentum between time t and time t+![]() t. Please note, this derivation neglects the effect of air resistance.
t. Please note, this derivation neglects the effect of air resistance.
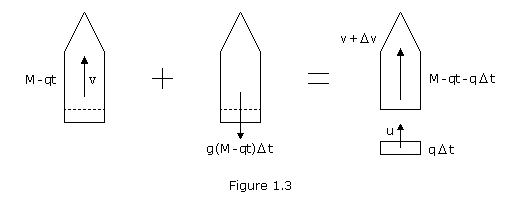
We write
![]()
We divide through by ![]() t and replace u-(v+
t and replace u-(v+![]() v) with Ve, the velocity of the expelled mass relative to the rocket. As
v) with Ve, the velocity of the expelled mass relative to the rocket. As ![]() t approaches zero, we obtain
t approaches zero, we obtain
![]()
Separating variables and integrating from t=0, v=0 to t=t, v=v, we obtain
![]()
which equals
![]()
The term -gt in equation (1.15) is the result of Earth's gravity pulling on the rocket. For a rocket drifting in space, -gt is not applicable and can be omitted. Furthermore, it is more appropriate to express the resulting velocity as a change in velocity, or ![]() V. Equation (1.15) thus becomes
V. Equation (1.15) thus becomes
![]()
Note that M represents the initial mass of the rocket and M-qt the final mass. Therefore, equation (1.16) is often written as
![]()
where mo/mf is called the mass ratio. Equation (1.17) is also known as Tsiolkovsky's rocket equation, named after Russian rocket pioneer Konstantin E. Tsiolkovsky (1857-1935) who first derived it.
In practical application, the variable Ve is usually replaced by the effective exhaust gas velocity, C. Equation (1.17) therefore becomes
![]()
Alternatively, we can write
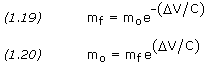
where e is a mathematical constant approximately equal to 2.71828.
For many spacecraft maneuvers it is necessary to calculate the duration of an engine burn required to achieve a specific change in velocity. Rearranging variables, we have
![]()
The combustion process involves the oxidation of constituents in the fuel that are capable of being oxidized, and can therefore be represented by a chemical equation. During a combustion process the mass of each element remains the same. Consider the reaction of methane with oxygen
![]()
This equation states that one mole of methane reacts with two moles of oxygen to form one mole of carbon dioxide and two moles of water. This also means that 16 g of methane react with 64 g of oxygen to form 44 g of carbon dioxide and 36 g of water. All the initial substances that undergo the combustion process are called the reactants, and the substances that result from the combustion process are called the products.
The above combustion reaction is an example of a stoichiometric mixture, that is, there is just enough oxygen present to chemically react with all the fuel. The highest flame temperature is achieved under these conditions, however it is often desirable to operate a rocket engine at a "fuel-rich" mixture ratio. Mixture ratio is defined as the mass flow of oxidizer divided by the mass flow of fuel.
Consider the following reaction of kerosene(1) with oxygen,
![]()
Given the molecular weight of C12H26 is 170 and that of O2 is 32, we have a mixture ratio of
![]()
which is typical of many rocket engines using kerosene, or RP-1, fuel.
The optimum mixture ratio is typically that which will deliver the highest engine performance (measured by specific impulse), however in some situations a different O/F ratio results in a better overall system. For a volume-constrained vehicle with a low-density fuel such as liquid hydrogen, significant reductions in vehicle size can be achieved by shifting to a higher O/F ratio. In that case, the losses in performance are more than compensated for by the reduced fuel tankage requirement. Also consider the example of bipropellant systems using NTO/MMH, where a mixture ratio of 1.67 results in fuel and oxidizer tanks of equal size. Equal sizing simplifies tank manufacturing, system packaging, and integration.
As we have seen previously, impulse thrust is equal to the product of the propellant mass flow rate and the exhaust gas ejection speed. The ideal exhaust velocity is given by
![]()
where k is the specific heat ratio, R* is the universal gas constant (8,314.4621 J/kmol-K in SI units, or 49,720 ft-lb/(slug-mol)-oR in U.S. units), Tc is the combustion temperature, M is the average molecular weight of the exhaust gases, Pc is the combustion chamber pressure, and Pe is the pressure at the nozzle exit.
Specific heat ratio(2) varies depending on the composition and temperature of the exhaust gases, but it is usually about 1.2. The thermodynamics involved in calculating combustion temperatures are quite complicated, however, flame temperatures generally range from about 2,500 to 3,600 oC (4,500-6,500 oF). Chamber pressures can range from about about 7 to 250 atmospheres. Pe should be equal to the ambient pressure at which the engine will operate, more on this later.
From equation (1.22) we see that high chamber temperature and pressure, and low exhaust gas molecular weight results in high ejection velocity, thus high thrust. Based on this criterion, we can see why liquid hydrogen is very desirable as a rocket fuel.
It should be pointed out that in the combustion process there will be a dissociation of molecules among the products. That is, the high heat of combustion causes the separation of molecules into simpler constituents that are then capable of recombining. Consider the reaction of kerosene with oxygen. The true products of combustion will be an equilibrium mixture of atoms and molecules consisting of C, CO, CO2, H, H2, H2O, HO, O, and O2. Dissociation has a significant effect on flame temperature.
If you wish to learn more about the thermodynamics of rockets engines, please consider reading the appendix Rocket Thermodynamics.
Or you can skip all the science and just look up the numbers you need. See Propellant Combustion Charts to find optimum mixture ratio, adiabatic flame temperature, gas molecular weight, and specific heat ratio for some common rocket propellants.
|
(1) In dealing with combustion of liquid hydrocarbon fuels it is convenient to express the composition in terms of a single hydrocarbon, even though it is a mixture of many hydrocarbons. Thus gasoline is usually considered to be octane, C8H18, and kerosene is considered to be dodecane, C12H26.
(2) Specific heat, or heat capacity, represents the amount of heat necessary to raise the temperature of one gram of a substance one degree C. Specific heat is measured at constant-pressure, CP, or at constant-volume, CV. The ratio CP/CV is called the specific heat ratio, represented by k or |
The specific impulse of a rocket, Isp, is the ratio of the thrust to the flow rate of the weight ejected, that is
![]()
where F is thrust, q is the rate of mass flow, and go is standard gravity (9.80665 m/s2).
Specific impulse is expressed in seconds. When the thrust and the flow rate remain constant throughout the burning of the propellant, the specific impulse is the time for which the rocket engine provides a thrust equal to the weight of the propellant consumed.
For a given engine, the specific impulse has different values on the ground and in the vacuum of space because the ambient pressure is involved in the expression for the thrust. It is therefore important to state whether specific impulse is the value at sea level or in a vacuum.
There are a number of losses within a rocket engine, the main ones being related to the inefficiency of the chemical reaction (combustion) process, losses due to the nozzle, and losses due to the pumps. Overall, the losses affect the efficiency of the specific impulse. This is the ratio of the real specific impulse (at sea level, or in a vacuum) and the theoretical specific impulse obtained with an ideal nozzle from gases coming from a complete chemical reaction. Calculated values of specific impulse are several percent higher than those attained in practice.
From Equation (1.8) we can substitute qC for F in Equation (1.23), thus obtaining
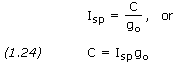
Equation (1.24) is very useful when solving Equations (1.18) through (1.21). It is rare we are given the value of C directly, however rocket engine specific impulse is a commonly given parameter from which we can easily calculate C.
Another important figure of merit for evaluating rocket performance is the characteristic exhaust velocity, C* (pronounced "C star"), which is a measure of the energy available from the combustion process and is given by
![]()
where Pc is the combustion chamber pressure and At is the area of the nozzle throat. Delivered values of C* range from about 1,333 m/s for monopropellant hydrazine up to about 2,360 m/s for cryogenic oxygen/hydrogen.
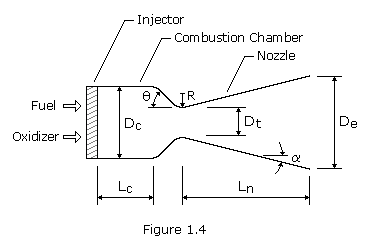 A typical rocket engine consists of the nozzle, the combustion chamber, and the injector, as shown in Figure 1.4. The combustion chamber is where the burning of propellants takes place at high pressure. The chamber must be strong enough to contain the high pressure generated by, and the high temperature resulting from, the combustion process. Because of the high temperature and heat transfer, the chamber and nozzle are usually cooled. The chamber must also be of sufficient length to ensure complete combustion before the gases enter the nozzle.
A typical rocket engine consists of the nozzle, the combustion chamber, and the injector, as shown in Figure 1.4. The combustion chamber is where the burning of propellants takes place at high pressure. The chamber must be strong enough to contain the high pressure generated by, and the high temperature resulting from, the combustion process. Because of the high temperature and heat transfer, the chamber and nozzle are usually cooled. The chamber must also be of sufficient length to ensure complete combustion before the gases enter the nozzle.
Nozzle
The function of the nozzle is to convert the chemical-thermal energy generated in the combustion chamber into kinetic energy. The nozzle converts the slow moving, high pressure, high temperature gas in the combustion chamber into high velocity gas of lower pressure and temperature. Since thrust is the product of mass and velocity, a very high gas velocity is desirable. Nozzles consist of a convergent and divergent section. The minimum flow area between the convergent and divergent section is called the nozzle throat. The flow area at the end of the divergent section is called the nozzle exit area. The nozzle is usually made long enough (or the exit area is great enough) such that the pressure in the combustion chamber is reduced at the nozzle exit to the pressure existing outside the nozzle. It is under this condition, Pe=Pa where Pe is the pressure at the nozzle exit and Pa is the outside ambient pressure, that thrust is maximum and the nozzle is said to be adapted, also called optimum or correct expansion. When Pe is greater than Pa, the nozzle is under-extended. When the opposite is true, it is over-extended.
We see therefore, a nozzle is designed for the altitude at which it has to operate. At the Earth's surface, at the atmospheric pressure of sea level (0.1 MPa or 14.7 psi), the discharge of the exhaust gases is limited by the separation of the jet from the nozzle wall. In the cosmic vacuum, this physical limitation does not exist. Therefore, there have to be two different types of engines and nozzles, those which propel the first stage of the launch vehicle through the atmosphere, and those which propel subsequent stages or control the orientation of the spacecraft in the vacuum of space.
The nozzle throat area, At, can be found if the total propellant flow rate is known and the propellants and operating conditions have been selected. Assuming perfect gas law theory, we have
![]()
where q is the propellant mass flow rate, Pt is the gas pressure at the nozzle throat, Tt is the gas temperature at the nozzle throat, R* is the universal gas constant, and k is the specific heat ratio. Pt and Tt are given by
![]()
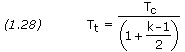
where Pc is the combustion chamber pressure and Tc is the combustion chamber flame temperature.
The hot gases must be expanded in the diverging section of the nozzle to obtain maximum thrust. The pressure of these gases will decrease as energy is used to accelerate the gas. We must find that area of the nozzle where the gas pressure is equal to the outside atmospheric pressure. This area will then be the nozzle exit area.
Mach number Nm is the ratio of the gas velocity to the local speed of sound. The Mach number at the nozzle exit is given by the perfect gas expansion expression
![]()
where Pa is the pressure of the ambient atmosphere.
The nozzle exit area, Ae, corresponding to the exit Mach number is given by
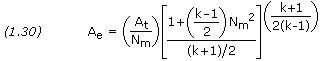
The section ratio, or expansion ratio, is defined as the area of the exit Ae divided by the area of the throat At.
For launch vehicles (particularly first stages) where the ambient pressure varies during the burn period, trajectory computations are performed to determine the optimum exit pressure. However, an additional constraint is the maximum allowable diameter for the nozzle exit cone, which in some cases is the limiting constraint. This is especially true on stages other than the first, where the nozzle diameter may not be larger than the outer diameter of the stage below. For space engines, where the ambient pressure is zero, thrust always increases as nozzle expansion ratio increases. On these engines, the nozzle expansion ratio is generally increased until the additional weight of the longer nozzle costs more performance than the extra thrust it generates.
(For additional information, please see Supplement #1: Optimizing Expansion for Maximum Thrust.)
Since the flow velocity of the gases in the converging section of the rocket nozzle is relatively low, any smooth and well-rounded convergent nozzle section will have very low energy loses. By contrast, the contour of the diverging nozzle section is very important to performance, because of the very high flow velocities involved. The selection of an optimum nozzle shape for a given expansion ratio is generally influenced by the following design considerations and goals: (1) uniform, parallel, axial gas flow at the nozzle exit for maximum momentum vector, (2) minimum separation and turbulence losses within the nozzle, (3) shortest possible nozzle length for minimum space envelope, weight, wall friction losses, and cooling requirements, and (4) ease of manufacturing.
Conical nozzle: In early rocket engine applications, the conical nozzle, which proved satisfactory in most respects, was used almost exclusively. A conical nozzle allows ease of manufacture and flexibility in converting an existing design to higher or lower expansion ratio without major redesign.
The configuration of a typical conical nozzle is shown in Figure 1.4. The nozzle throat section has the contour of a circular arc with radius R, ranging from 0.25 to 0.75 times the throat diameter, Dt. The half-angle of the nozzle convergent cone section, ![]() , can range from 20 to 45 degrees. The divergent cone half-angle,
, can range from 20 to 45 degrees. The divergent cone half-angle, ![]() , varies from approximately 12 to 18 degrees. The conical nozzle with a 15-degree divergent half-angle has become almost a standard because it is a good compromise on the basis of weight, length, and performance.
, varies from approximately 12 to 18 degrees. The conical nozzle with a 15-degree divergent half-angle has become almost a standard because it is a good compromise on the basis of weight, length, and performance.
Since certain performance losses occur in a conical nozzle as a result of the nonaxial component of the exhaust gas velocity, a correction factor, ![]() , is applied in the calculation of the exit-gas momentum. This factor (thrust efficiency) is the ratio between the exit-gas momentum of the conical nozzle and that of an ideal nozzle with uniform, parallel, axial gas-flow. The value of
, is applied in the calculation of the exit-gas momentum. This factor (thrust efficiency) is the ratio between the exit-gas momentum of the conical nozzle and that of an ideal nozzle with uniform, parallel, axial gas-flow. The value of ![]() can be expressed by the following equation:
can be expressed by the following equation:
![]()
 Bell nozzle: To gain higher performance and shorter length, engineers developed the bell-shaped nozzle. It employs a fast-expansion (radial-flow) section in the initial divergent region, which leads to a uniform, axially directed flow at the nozzle exit. The wall contour is changed gradually enough to prevent oblique shocks.
Bell nozzle: To gain higher performance and shorter length, engineers developed the bell-shaped nozzle. It employs a fast-expansion (radial-flow) section in the initial divergent region, which leads to a uniform, axially directed flow at the nozzle exit. The wall contour is changed gradually enough to prevent oblique shocks.
An equivalent 15-degree half-angle conical nozzle is commonly used as a standard to specify bell nozzles. For instance, the length of an 80% bell nozzle (distance between throat and exit plane) is 80% of that of a 15-degree half-angle conical nozzle having the same throat area, radius below the throat, and area expansion ratio. Bell nozzle lengths beyond approximately 80% do not significantly contribute to performance, especially when weight penalties are considered. However, bell nozzle lengths up to 100% can be optimum for applications stressing very high performance.
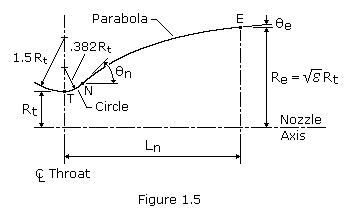
One convenient way of designing a near optimum thrust bell nozzle contour uses the parabolic approximation procedures suggested by G.V.R. Rao. The design configuration of a parabolic approximation bell nozzle is shown in Figure 1.5. The nozzle contour immediately upstream of the throat T is a circular arc with a radius of 1.5 Rt. The divergent section nozzle contour is made up of a circular entrance section with a radius of 0.382 Rt from the throat T to the point N and parabola from there to the exit E.
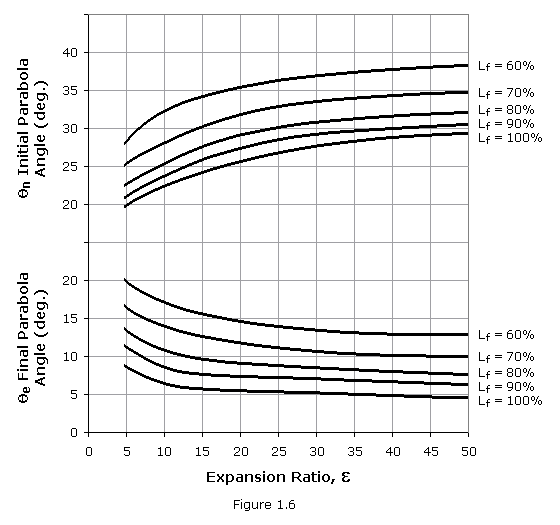
Design of a specific nozzle requires the following data: throat diameter Dt, axial length of the nozzle from throat to exit plane Ln (or the desired fractional length, Lf, based on a 15-degree conical nozzle), expansion ratio ![]() , initial wall angle of the parabola
, initial wall angle of the parabola ![]() n, and nozzle exit wall angle
n, and nozzle exit wall angle ![]() e. The wall angles
e. The wall angles ![]() n and
n and ![]() e are shown in Figure 1.6 as a function of the expansion ratio. Optimum nozzle contours can be approximated very accurately by selecting the proper inputs. Although no allowance is made for different propellant combinations, experience has shown only small effect of the specific heat ratio upon the contour.
e are shown in Figure 1.6 as a function of the expansion ratio. Optimum nozzle contours can be approximated very accurately by selecting the proper inputs. Although no allowance is made for different propellant combinations, experience has shown only small effect of the specific heat ratio upon the contour.
Combustion Chamber
The combustion chamber serves as an envelope to retain the propellants for a sufficient period to ensure complete mixing and combustion. The required stay time, or combustion residence time, is a function of many parameters. The theoretically required combustion chamber volume is a function of the mass flow rate of the propellants, the average density of the combustion products, and the stay time needed for efficient combustion. This relationship can be expressed by the following equation:
![]()
where Vc is the chamber volume, q is the propellant mass flow rate, V is the average specific volume, and ts is the propellant stay-time.
A useful parameter relative to chamber volume and residence time is the characteristic length, L* (pronounced "L star"), the chamber volume divided by the nozzle sonic throat area:
![]()
The L* concept is much easier to visualize than the more elusive "combustion residence time", expressed in small fractions of a second. Since the value of At is in nearly direct proportion to the product of q and V, L* is essentially a function of ts.
The customary method of establishing the L* of a new thrust chamber design largely relies on past experience with similar propellants and engine size. Under a given set of operating conditions, such as type of propellant, mixture ratio, chamber pressure, injector design, and chamber geometry, the value of the minimum required L* can only be evaluated by actual firings of experimental thrust chambers. Typical L* values for various propellants are shown in the table below. With throat area and minimum required L* established, the chamber volume can be calculated by equation (1.33).
| Propellant Combination | L*, cm |
|---|---|
| Nitric acid/hydrazine-base fuel | 76-89 |
| Nitrogen tetroxide/hydrazine-base fuel | 76-89 |
| Hydrogen peroxide/RP-1 (including catalyst bed) | 152-178 |
| Liquid oxygen/RP-1 | 102-127 |
| Liquid oxygen/ammonia | 76-102 |
| Liquid oxygen/liquid hydrogen (GH2 injection) | 56-71 |
| Liquid oxygen/liquid hydrogen (LH2 injection) | 76-102 |
| Liquid fluorine/liquid hydrogen (GH2 injection) | 56-66 |
| Liquid fluorine/liquid hydrogen (LH2 injection) | 64-76 |
| Liquid fluorine/hydrazine | 61-71 |
| Chlorine trifluoride/hydrazine-base fuel | 51-89 |
Three geometrical shapes have been used in combustion chamber design - spherical, near-spherical, and cylindrical - with the cylindrical chamber being employed most frequently in the United States. Compared to a cylindrical chamber of the same volume, a spherical or near-spherical chamber offers the advantage of less cooling surface and weight; however, the spherical chamber is more difficult to manufacture and has provided poorer performance in other respects.
The total combustion process, from injection of the reactants until completion of the chemical reactions and conversion of the products into hot gases, requires finite amounts of time and volume, as expressed by the characteristic length L*. The value of this factor is significantly greater than the linear length between injector face and throat plane. The contraction ratio is defined as the major cross-sectional area of the combuster divided by the throat area. Typically, large engines are constructed with a low contraction ratio and a comparatively long length; and smaller chambers employ a large contraction ratio with a shorter length, while still providing sufficient L* for adequate vaporization and combustion dwell-time.
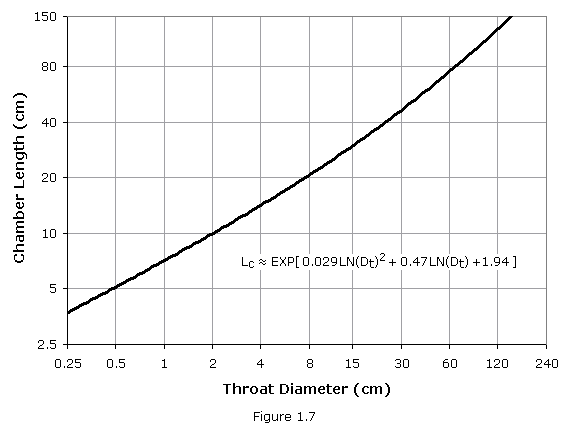
As a good place to start, the process of sizing a new combustion chamber examines the dimensions of previously successful designs in the same size class and plotting such data in a rational manner. The throat size of a new engine can be generated with a fair degree of confidence, so it makes sense to plot the data from historical sources in relation to throat diameter. Figure 1.7 plots chamber length as a function of throat diameter (with approximating equation). It is important that the output of any modeling program not be slavishly applied, but be considered a logical starting point for specific engine sizing.
The basic elements of a cylindrical thrust-chamber are identified in Figure 1.4. In design practice, it has been arbitrarily defined that the combustion chamber volume includes the space between the injector face and the nozzle throat plane. The approximate volume of the combustion chamber can be expressed by the following equation:
![]()
Rearranging equation (1.34) we get the following, which can be solved for the chamber diameter via iteration:
![]()
Injector
The injector, as the name implies, injects the propellants into the combustion chamber in the right proportions and the right conditions to yield an efficient, stable combustion process. Placed at the forward, or upper, end of the combustor, the injector also performs the structural task of closing off the top of the combustion chamber against the high pressure and temperature it contains. The injector has been compared to the carburetor of an automobile engine, since it provides the fuel and oxidizer at the proper rates and in the correct proportions, this may be an appropriate comparison. However, the injector, located directly over the high-pressure combustion, performs many other functions related to the combustion and cooling processes and is much more important to the function of the rocket engine than the carburetor is for an automobile engine.
No other component of a rocket engine has as great an impact upon engine performance as the injector. In various and different applications, well-designed injectors may have a fairly wide spread in combustion efficiency, and it is not uncommon for an injector with C* efficiency as low as 92% to be considered acceptable. Small engines designed for special purposes, such as attitude control, may be optimized for response and light weight at the expense of combustion efficiency, and may be deemed very satisfactory even if efficiency falls below 90%. In general, however, recently well-designed injection systems have demonstrated C* efficiencies so close to 100% of theoretical that the ability to measure this parameter is the limiting factor in its determination. High levels of combustion efficiency derive from uniform distribution of the desired mixture ratio and fine atomization of the liquid propellants. Local mixing within the injection-element spray pattern must take place at virtually a microscopic level to ensure combustion efficiencies approaching 100%.
Combustion stability is also a very important requirement for a satisfactory injector design. Under certain conditions, shock and detonation waves are generated by local disturbances in the chamber, possibly caused by fluctuations in mixing or propellant flow. These may trigger pressure oscillations that are amplified and maintained by the combustion processes. Such high-amplitude waves - referred to as combustion instability - produce high levels of vibration and heat flux that can be very destructive. A major portion of the design and development effort therefore concerns stable combustion. High performance can become secondary if the injector is easily triggered into destructive instability, and many of the injector parameters that provide high performance appear to reduce the stability margin.
Liquid bipropellant rocket engines can be categorized according to their power cycles, that is, how power is derived to feed propellants to the main combustion chamber. Described below are some of the more common types.
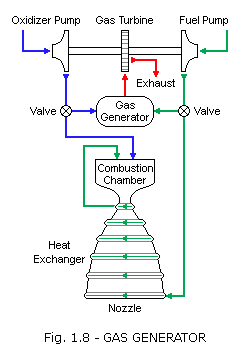
Gas-generator cycle: The gas-generator cycle, also called open cycle, taps off a small amount of fuel and oxidizer from the main flow (typically 2 to 7 percent) to feed a burner called a gas generator. The hot gas from this generator passes through a turbine to generate power for the pumps that send propellants to the combustion chamber. The hot gas is then either dumped overboard or sent into the main nozzle downstream. Increasing the flow of propellants into the gas generator increases the speed of the turbine, which increases the flow of propellants into the main combustion chamber, and hence, the amount of thrust produced. The gas generator must burn propellants at a less-than-optimal mixture ratio to keep the temperature low for the turbine blades. Thus, the cycle is appropriate for moderate power requirements but not high-power systems, which would have to divert a large portion of the main flow to the less efficient gas-generator flow.
As in most rocket engines, some of the propellant in a gas generator cycle is used to cool the nozzle and combustion chamber, increasing efficiency and allowing higher engine temperature.
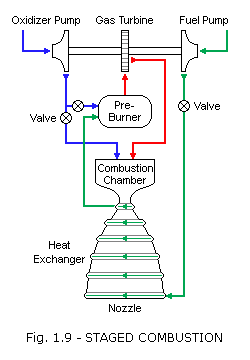
Staged combustion cycle: In a staged combustion cycle, also called closed cycle, the propellants are burned in stages. Like the gas-generator cycle, this cycle also has a burner, called a preburner, to generate gas for a turbine. The preburner taps off and burns a small amount of one propellant and a large amount of the other, producing an oxidizer-rich or fuel-rich hot gas mixture that is mostly unburned vaporized propellant. This hot gas is then passed through the turbine, injected into the main chamber, and burned again with the remaining propellants. The advantage over the gas-generator cycle is that all of the propellants are burned at the optimal mixture ratio in the main chamber and no flow is dumped overboard. The staged combustion cycle is often used for high-power applications. The higher the chamber pressure, the smaller and lighter the engine can be to produce the same thrust. Development cost for this cycle is higher because the high pressures complicate the development process. Further disadvantages are harsh turbine conditions, high temperature piping required to carry hot gases, and a very complicated feedback and control design.
Staged combustion was invented by Soviet engineers and first appeared in 1960. In the West, the first laboratory staged combustion test engine was built in Germany in 1963.
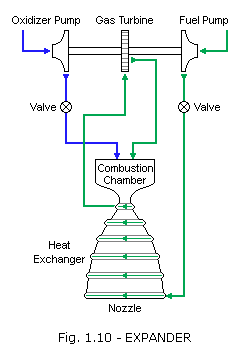
Expander cycle: The expander cycle is similar to the staged combustion cycle but has no preburner. Heat in the cooling jacket of the main combustion chamber serves to vaporize the fuel. The fuel vapor is then passed through the turbine and injected into the main chamber to burn with the oxidizer. This cycle works with fuels such as hydrogen or methane, which have a low boiling point and can be vaporized easily. As with the staged combustion cycle, all of the propellants are burned at the optimal mixture ratio in the main chamber, and typically no flow is dumped overboard; however, the heat transfer to the fuel limits the power available to the turbine, making this cycle appropriate for small to midsize engines. A variation of the system is the open, or bleed, expander cycle, which uses only a portion of the fuel to drive the turbine. In this variation, the turbine exhaust is dumped overboard to ambient pressure to increase the turbine pressure ratio and power output. This can achieve higher chamber pressures than the closed expander cycle although at lower efficiency because of the overboard flow.
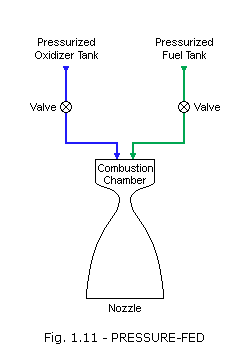
Pressure-fed cycle: The simplest system, the pressure-fed cycle, does not have pumps or turbines but instead relies on tank pressure to feed the propellants into the main chamber. In practice, the cycle is limited to relatively low chamber pressures because higher pressures make the vehicle tanks too heavy. The cycle can be reliable, given its reduced part count and complexity compared with other systems.
The heat created during combustion in a rocket engine is contained within the exhaust gases. Most of this heat is expelled along with the gas that contains it; however, heat is transferred to the thrust chamber walls in quantities sufficient to require attention.
Thrust chamber designs are generally categorized or identified by the hot gas wall cooling method or the configuration of the coolant passages, where the coolant pressure inside may be as high as 500 atmospheres. The high combustion temperatures (2,500 to 3,600o K) and the high heat transfer rates (up to 16 kJ/cm2-s) encountered in a combustion chamber present a formidable challenge to the designer. To meet this challenge, several chamber cooling techniques have been utilized successfully. Selection of the optimum cooling method for a thrust chamber depends on many considerations, such as type of propellant, chamber pressure, available coolant pressure, combustion chamber configuration, and combustion chamber material.
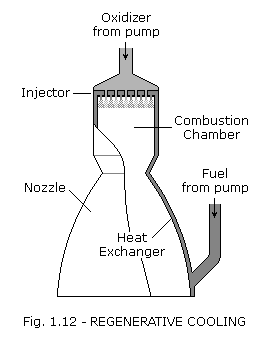 Regenerative cooling is the most widely used method of cooling a thrust chamber and is accomplished by flowing high-velocity coolant over the back side of the chamber hot gas wall to convectively cool the hot gas liner. The coolant with the heat input from cooling the liner is then discharged into the injector and utilized as a propellant.
Regenerative cooling is the most widely used method of cooling a thrust chamber and is accomplished by flowing high-velocity coolant over the back side of the chamber hot gas wall to convectively cool the hot gas liner. The coolant with the heat input from cooling the liner is then discharged into the injector and utilized as a propellant.
Earlier thrust chamber designs, such as the V-2 and Redstone, had low chamber pressure, low heat flux and low coolant pressure requirements, which could be satisfied by a simplified "double wall chamber" design with regenerative and film cooling. For subsequent rocket engine applications, however, chamber pressures were increased and the cooling requirements became more difficult to satisfy. It became necessary to design new coolant configurations that were more efficient structurally and had improved heat transfer characteristics.
This led to the design of "tubular wall" thrust chambers, by far the most widely used design approach for the vast majority of large rocket engine applications. These chamber designs have been successfully used for the Thor, Jupiter, Atlas, H-1, J-2, F-1, RS-27 and several other Air Force and NASA rocket engine applications. The primary advantage of the design is its light weight and the large experience base that has accrued. But as chamber pressures and hot gas wall heat fluxes have continued to increase (>100 atm), still more effective methods have been needed.
One solution has been "channel wall" thrust chambers, so named because the hot gas wall cooling is accomplished by flowing coolant through rectangular channels, which are machined or formed into a hot gas liner fabricated from a high-conductivity material, such as copper or a copper alloy. A prime example of a channel wall combustion chamber is the SSME, which operates at 204 atmospheres nominal chamber pressure at 3,600 K for a duration of 520 seconds. Heat transfer and structural characteristics are excellent.
In addition to the regeneratively cooled designs mentioned above, other thrust chamber designs have been fabricated for rocket engines using dump cooling, film cooling, transpiration cooling, ablative liners and radiation cooling. Although regeneratively cooled combustion chambers have proven to be the best approach for cooling large liquid rocket engines, other methods of cooling have also been successfully used for cooling thrust chamber assemblies. Examples include:
Dump cooling, which is similar to regenerative cooling because the coolant flows through small passages over the back side of the thrust chamber wall. The difference, however, is that after cooling the thrust chamber, the coolant is discharged overboard through openings at the aft end of the divergent nozzle. This method has limited application because of the performance loss resulting from dumping the coolant overboard. To date, dump cooling has not been used in an actual application.
Film cooling provides protection from excessive heat by introducing a thin film of coolant or propellant through orifices around the injector periphery or through manifolded orifices in the chamber wall near the injector or chamber throat region. This method is typically used in high heat flux regions and in combination with regenerative cooling.
Transpiration cooling provides coolant (either gaseous or liquid propellant) through a porous chamber wall at a rate sufficient to maintain the chamber hot gas wall to the desired temperature. The technique is really a special case of film cooling.
With ablative cooling, combustion gas-side wall material is sacrificed by melting, vaporization and chemical changes to dissipate heat. As a result, relatively cool gases flow over the wall surface, thus lowering the boundary-layer temperature and assisting the cooling process.
With radiation cooling, heat is radiated from the outer surface of the combustion chamber or nozzle extension wall. Radiation cooling is typically used for small thrust chambers with a high-temperature wall material (refractory) and in low-heat flux regions, such as a nozzle extension.
Solid rockets motors store propellants in solid form. The fuel is typically powdered aluminum and the oxidizer is ammonium perchlorate. A synthetic rubber binder such as polybutadiene holds the fuel and oxidizer powders together. Though lower performing than liquid propellant rockets, the operational simplicity of a solid rocket motor often makes it the propulsion system of choice.
Solid Fuel Geometry
A solid fuel's geometry determines the area and contours of its exposed surfaces, and thus its burn pattern. There are two main types of solid fuel blocks used in the space industry. These are cylindrical blocks, with combustion at a front, or surface, and cylindrical blocks with internal combustion. In the first case, the front of the flame travels in layers from the nozzle end of the block towards the top of the casing. This so-called end burner produces constant thrust throughout the burn. In the second, more usual case, the combustion surface develops along the length of a central channel. Sometimes the channel has a star shaped, or other, geometry to moderate the growth of this surface.
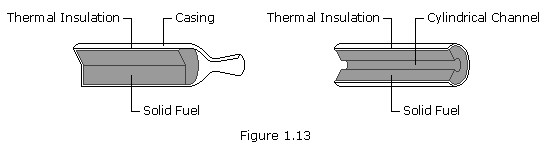
The shape of the fuel block for a rocket is chosen for the particular type of mission it will perform. Since the combustion of the block progresses from its free surface, as this surface grows, geometrical considerations determine whether the thrust increases, decreases or stays constant.
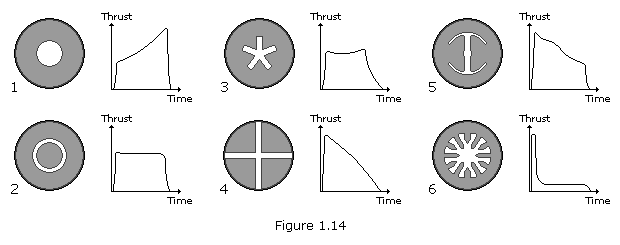
Fuel blocks with a cylindrical channel (1) develop their thrust progressively. Those with a channel and also a central cylinder of fuel (2) produce a relatively constant thrust, which reduces to zero very quickly when the fuel is used up. The five pointed star profile (3) develops a relatively constant thrust which decreases slowly to zero as the last of the fuel is consumed. The 'cruciform' profile (4) produces progressively less thrust. Fuel in a block with a 'double anchor' profile (5) produces a decreasing thrust which drops off quickly near the end of the burn. The 'cog' profile (6) produces a strong inital thrust, followed by an almost constant lower thrust.
Burn Rate
The burning surface of a rocket propellant grain recedes in a direction perpendicular to this burning surface. The rate of regression, typically measured in millimeters per second (or inches per second), is termed burn rate. This rate can differ significantly for different propellants, or for one particular propellant, depending on various operating conditions as well as formulation. Knowing quantitatively the burning rate of a propellant, and how it changes under various conditions, is of fundamental importance in the successful design of a solid rocket motor.
Propellant burning rate is influenced by certain factors, the most significant being: combustion chamber pressure, initial temperature of the propellant grain, velocity of the combustion gases flowing parallel to the burning surface, local static pressure, and motor acceleration and spin. These factors are discussed below.
where r is the burn rate, a is the burn rate coefficient, n is the pressure exponent, and Pc is the combustion chamber pressure. The values of a and n are determined empirically for a particular propellant formulation and cannot be theoretically predicted. It is important to realize that a single set of a, n values are typically valid over a distinct pressure range. More than one set may be necessary to accurately represent the full pressure regime of interest.
Example a, n values are 0.0445289* (pressure in pascals, burn rate in mm/s) and 0.35 respectively for the Space Shuttle SRBs, which gives a burn rate of 9.34 mm/s at the average chamber pressure of 4.3 MPa.
* NASA publications gives a burn rate coefficient of 0.0386625 (pressure in PSI, burn rate in inch/s). The effects of erosive burning can be minimized by designing the motor with a sufficiently large port-to-throat area ratio (Aport/At). The port area is the cross-section area of the flow channel in a motor. For a hollow-cylindrical grain, this is the cross-section area of the core. As a rule of thumb, the ratio should be a minimum of 2 for a grain L/D ratio of 6. A greater Aport/At ratio should be used for grains with larger L/D ratios.
![]()
It is sometimes desirable to modify the burning rate such that it is more suitable to a certain grain configuration. For example, if one wished to design an end burner grain, which has a relatively small burning area, it is necessary to have a fast burning propellant. In other circumstances, a reduced burning rate may be sought after. For example, a motor may have a large L/D ratio to generate sufficiently high thrust, or it may be necessary for a particular design to restrict the diameter of the motor. The web would be consequently thin, resulting in short burn duration. Reducing the burning rate would be beneficial.
There are a number of ways of modifying the burning rate: decrease the oxidizer particle size, increase or reduce the percentage of oxidizer, adding a burn rate catalyst or suppressant, and operate the motor at a lower or higher chamber pressure. These factors are discussed below.
Product Generation Rate
The rate at which combustion products are generated is expressed in terms of the regression speed of the grain. The product generation rate integrated over the port surface area is
![]()
where q is the combustion product generation rate at the propellant surface, ![]() p is the solid propellant density, Ab is the area of the burning surface, and r is the propellant burn rate.
p is the solid propellant density, Ab is the area of the burning surface, and r is the propellant burn rate.
If the propellant density is unknown, it can be derived from the mass fraction and density of the individual constituents, as follows:
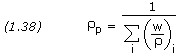
where w is the mass fraction and the subscript i denotes the individual constituents. This is the ideal density; the actual density is typically 94%-97% of the ideal density, owing to tiny voids in the grain, and is dependant upon the manufacturing technique.
Condensed-Phase Mass
It is important to note that the combustion products may consist of both gaseous and condensed-phase mass. The condensed-phase, which manifests itself as smoke, may be either solid or liquid particles. Only the gaseous products contribute to pressure development. The condensed-phase certainly does, however, contribute to the thrust of the rocket motor, due to its mass and velocity.
The occurrence of solids or liquids in a rocket's exhaust leads to a reduction in performance for a number of reasons:
Chamber Pressure
The pressure curve of a rocket motor exhibits transient and steady state behavior. The transient phases are when the pressure varies substantially with time – during the ignition and start-up phase, and following complete (or nearly complete) grain consumption when the pressure falls down to ambient level during the tail-off phase. The variation of chamber pressure during the steady state burning phase is due mainly to variation of grain geometry with associated burn rate variation. Other factors may play a role, however, such as nozzle throat erosion and erosive burn rate augmentation.
By far the most widely used type of propulsion for spacecraft attitude and velocity control is monopropellant hydrazine. Its excellent handling characteristics, relative stability under normal storage conditions, and clean decomposition products have made it the standard. The general sequence of operations in a hydrazine thruster is:
Monopropellant hydrazine thrusters typically produce a specific impulse of about 230 to 240 seconds.
Other suitable propellants for catalytic decomposition engines are hydrogen peroxide and nitrous oxide, however the performance is considerably lower than that obtained with hydrazine - specific impulse of about 150 s with H2O2 and about 170 s with N2O.
Monopropellant systems have successfully provided orbit maintenance and attitude control functions, but lack the performance to provide weight-efficient large ![]() V maneuvers required for orbit insertion. Bipropellant systems are attractive because they can provide all three functions with one higher performance system, but they are more complex than the common solid rocket and monopropellant combined systems. A third alternative are dual mode systems. These systems are hybrid designs that use hydrazine both as a fuel for high performance bipropellant engines and as a monopropellant with conventional low-thrust catalytic thrusters. The hydrazine is fed to both the bipropellant engines and the monopropellant thrusters from a common fuel tank.
V maneuvers required for orbit insertion. Bipropellant systems are attractive because they can provide all three functions with one higher performance system, but they are more complex than the common solid rocket and monopropellant combined systems. A third alternative are dual mode systems. These systems are hybrid designs that use hydrazine both as a fuel for high performance bipropellant engines and as a monopropellant with conventional low-thrust catalytic thrusters. The hydrazine is fed to both the bipropellant engines and the monopropellant thrusters from a common fuel tank.
Cold gas propulsion is just a controlled, pressurized gas source and a nozzle. It represents the simplest form of rocket engine. Cold gas has many applications where simplicity and/or the need to avoid hot gases are more important than high performance. The Manned Maneuvering Unit used by astronauts is an example of such a system.
Multistage rockets allow improved payload capability for vehicles with a high ![]() V requirement such as launch vehicles or interplanetary spacecraft. In a multistage rocket, propellant is stored in smaller, separate tanks rather than a larger single tank as in a single-stage rocket. Since each tank is discarded when empty, energy is not expended to accelerate the empty tanks, so a higher total
V requirement such as launch vehicles or interplanetary spacecraft. In a multistage rocket, propellant is stored in smaller, separate tanks rather than a larger single tank as in a single-stage rocket. Since each tank is discarded when empty, energy is not expended to accelerate the empty tanks, so a higher total ![]() V is obtained. Alternatively, a larger payload mass can be accelerated to the same total
V is obtained. Alternatively, a larger payload mass can be accelerated to the same total ![]() V. For convenience, the separate tanks are usually bundled with their own engines, with each discardable unit called a stage.
V. For convenience, the separate tanks are usually bundled with their own engines, with each discardable unit called a stage.
Multistage rocket performance is described by the same rocket equation as single-stage rockets, but must be determined on a stage-by-stage basis. The velocity increment, ![]() Vi, for each stage is calculated as before,
Vi, for each stage is calculated as before,
![]()
where moi represents the total vehicle mass when stage i is ignited, and mfi is the total vehicle mass when stage i is burned out but not yet discarded. It is important to realize that the payload mass for any stage consists of the mass of all subsequent stages plus the ultimate payload itself. The velocity increment for the vehicle is then the sum of those for the individual stages where n is the total number of stages.
![]()
We define the payload fraction as the ratio of payload mass to initial mass, or mpl/mo.
For a multistage vehicle with dissimilar stages, the overall vehicle payload fraction depends on how the ![]() V requirement is partitioned among stages. Payload fractions will be reduced if the
V requirement is partitioned among stages. Payload fractions will be reduced if the ![]() V is partitioned suboptimally. The optimal distribution may be determined by trial and error. A
V is partitioned suboptimally. The optimal distribution may be determined by trial and error. A ![]() V distribution is postulated and the resulting payload fraction calculated. The
V distribution is postulated and the resulting payload fraction calculated. The ![]() V distribution is varied until the payload fraction is maximized. Once the
V distribution is varied until the payload fraction is maximized. Once the ![]() V distribution is selected, vehicle sizing is accomplished by starting with the uppermost or final stage (whose payload is the actual deliverable payload) and calculating the initial mass of this assembly. This assembly then forms the payload for the previous stage and the process repeats until all stages are sized. Results reveal that to maximize payload fraction for a given
V distribution is selected, vehicle sizing is accomplished by starting with the uppermost or final stage (whose payload is the actual deliverable payload) and calculating the initial mass of this assembly. This assembly then forms the payload for the previous stage and the process repeats until all stages are sized. Results reveal that to maximize payload fraction for a given ![]() V requirement:
V requirement:
1. Stages with higher Isp should be above stages with lower Isp.
2. More ![]() V should be provided by the stages with the higher Isp.
V should be provided by the stages with the higher Isp.
3. Each succeeding stage should be smaller than its predecessor.
4. Similar stages should provide the same ![]() V.
V.
Compiled, edited and written in part by Robert A. Braeunig, 1997, 2005, 2007, 2009, 2012.
Bibliography